真真

真真

回覆: 1

2021-04-19 7:46 pm

整數n的s進制表示為777,若n為某整數的四次方,問s最小值為何?

真真

回覆: 1

2021-04-19 7:27 pm

若n是正整數,證明n(n+1)不為立方數?

真真

回覆: 1

2021-04-19 7:11 pm

若x,y,z為正實數滿足x+y+z≧xyz,證明x ²+y²+z²≧xyz?

真真

回覆: 1

2021-04-17 10:32 pm

是否存在三個成等比數列的整數x,y,z使十進制數n=x³+y³+z³-3xyz之末兩位數字是20?

真真

回覆: 2

2021-04-17 10:23 pm

對一切正整數n有f(n+2)=(n+3)*f(n+1)-(n+2)*f(n),若f(1)=1,f(2)=3,求所有為11倍數的f(n)之值?

真真

回覆: 1

2021-04-16 9:16 pm

求證無論在12008的兩個0之間添加多少個3,都能被19整除?

真真

回覆: 1

2021-04-16 9:07 pm

證明: x為有理數的充分必要條件是等差數列x,x+1,x+2,x+3,...中有三個不同的項構成等比數列?

真真

回覆: 1

2021-04-16 7:47 pm

一數列的通項a(n)滿足a(1)=1,a(n+1)=a(n)+1/a(n),問a(100)之值整數部分為何?

真真

回覆: 2

2021-04-14 10:08 pm

若x,y為實數,求所有滿足恆等式sinx+cosy=f(x)+f(y)+g(x)-g(y)的函數f(x)和g(x)?

真真

回覆: 1

2021-04-14 9:29 pm

一數列的通項a(n)滿足遞推關係a(n+1)=3a(n)-2n²+4n+4,且a(1)=1,求通項a(n)的表示式?

真真

回覆: 1

2021-03-20 9:59 pm

a1,a2,...,an為正等比數列,已知S=a1+a2+...+an,T=1/a1+1/a2+...+1/an,試以S,T和n表a1*a2*...*an?

真真

回覆: 2

2021-03-20 9:50 pm

一個正數列的通項為an,前n項和Sn=(an+(1/an))/2,求通項an的表示式?

真真

回覆: 1

2021-03-18 8:25 pm

已知數列a1=a2=1,且a(n+2)-a(n)=1/a(n+1),求a(2020)?

真真

回覆: 1

2021-03-18 6:22 pm

已f(1)+f(2)+...+f(n)=n²f(n), 若f(1)=1010,求f(2020)之值?

真真

回覆: 1

2021-02-08 11:12 pm

求所有自然數n使26.5^n+37.5^n為正整數?

真真

回覆: 3

2021-02-08 11:07 pm

求所有正整數n使1+2^n+3^n+4^n被5整除?

真真

回覆: 0

2021-02-08 11:00 pm

一羣7至13歲的兒童來自11個國家,證明必能從中找到5位兒童, 每位的同齡人多於其同國籍的人?

真真

回覆: 1

2021-02-06 10:41 pm

若a,b,c,d為不同整數,且(x-a)(x-b)(x-c)(x-d)-4=0有一整數根q,求a+b+c+d-4q之值?

真真

回覆: 0

2021-02-06 10:33 pm

平面上標有多個不共線的點,並在每點上記一個實數,已知任何一條過兩個或以上標點的直線上所有標點記的數之和皆為0,證明:平面上所有實數之和是0?

真真

回覆: 1

2021-02-06 10:18 pm

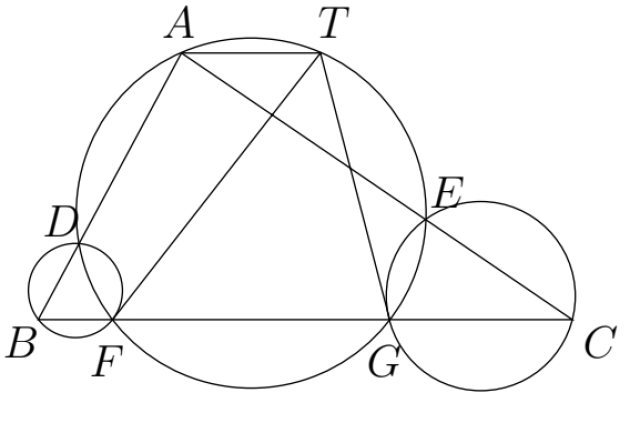
如圖,一圓交三角形ABC於點A,D,F,G,E,而過點F的圓BDF的切線和過點G的圓CEG的切線交於T,若A和T不重合,證明AT//BC?

真真

回覆: 2

2021-02-06 9:59 pm

從整數1至2020中選取四個數使其中兩個數之和等於另兩個數之和有幾種方法?

真真

回覆: 1

2021-01-14 9:49 pm

求出所有正整數對(m,n),使 1+x^n+x^(2n)+....+x^(mn)能被1+x+x^2+....+x^m整除?

真真

回覆: 1

2021-01-14 9:40 pm

圓上有n個點,連結此n個點依次記為p1,p2,...pn,問使折線p1p2...pn不自交的連法有幾種?

真真

回覆: 1

2021-01-14 9:19 pm

若a,b,c,d是整數,已知ac,bc+ad和bd有公因數e,問bc和ad是否也有公因數e?

真真

回覆: 1

2021-01-14 9:15 pm

在x,y的正半軸上各有m個和n個定點,在此m及n個點中每兩點連一直線,若無三線共點,問全部所連線段交點總數為何(線段端點不計)?

真真

回覆: 1

2020-12-21 8:53 pm

對所有奇素數p,求證2/p有且僅有一種方法表為2/p=1/x+1/y之形式,其中x,y為相異正整數?

真真

回覆: 1

2020-12-21 8:45 pm

若x^n=x+1,y^2n=3x+y,已知n為不小於2的整數,求證x>y?

真真

回覆: 1

2020-12-21 8:17 pm

某凸n邊形的任兩條對角線不平行且無三條對角線共點,把所有對角線兩面延申,問形外得幾交點?

真真

回覆: 1

2020-12-20 10:03 pm

求最大的自然數n使之能整除(7^m)+12m-1,其中m為任何自然數?

真真

回覆: 1

2020-12-20 9:36 pm

正實數x,y,z滿足xyz=1,問x³/[(y+1)(z+1)]+y³/[(z+1)(x+1)]+z³/[(x+1)(y+1)]之最小值為何?

真真

回覆: 1

2020-12-20 9:34 pm

圓上有n個點,連結此n個點依次記為p1,p2,...pn,問使折線p1p2...pn不自交的連法有幾種?

真真

回覆: 1

2020-12-05 5:35 pm

99條直線把平面分成n部分,若n<199,求n的所有可能值?

真真

回覆: 1

2020-11-29 11:22 pm

設f(x)=ax²+bx+c,若f(1),f(2),f(3),f(4),f(5)都是質數,求證f(x)不能分解為兩個整係數一次式之積?

真真

回覆: 1

2020-11-29 11:12 pm

求證24個不小於5的質數之平方和能被24整除?

真真

回覆: 1

2020-11-29 11:03 pm

若x²+5x+16被169整除,證明 x不是整數?

真真

回覆: 0

2020-11-29 7:30 pm

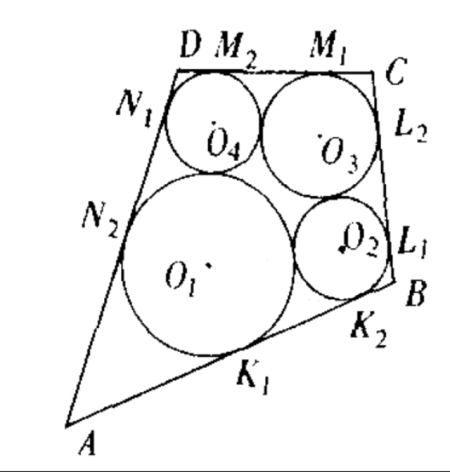
如圖,在凸四邊形ABCD內的四個小圓各自與四邊形的兩條邊及另外兩個小圓相切,已知四邊形ABCD含有內切圓,證明上述四個小圓中至少有兩個相等?

真真

回覆: 1

2020-09-19 2:52 pm

正實數x,y,z滿足xyz=1,問x³/[(y+1)(z+1)]+y³/[(z+1)(x+1)]+z³/[(x+1)(y+ 1)]之最小值為何? 若A,B,C是三角形的三個內角,問cosA+cosB+cosC和sin(A/2)+sin(B/2)+sin(C/2)之大小關係如何?

真真

回覆: 1

2020-07-18 10:06 pm

有1999個共線點,以這些點為端點的所有線段中,至少有幾個不同的中點?

真真

回覆: 1

2020-07-18 9:46 pm

求和:-(C(2n,1))²+(C(2n,2))²-.....+((-1)^(n-1))(C(2n,n-1))²+((-1)^n)(C(2n,n))²=?

真真

回覆: 1

2020-06-25 11:06 pm

求和:C(n,1)-(1/2)C(n,2)+(1/3)C(n,3)-.....+((-1)^(n-1))(1/n)C(n,n)=?

真真

回覆: 1

2020-06-22 9:04 pm

求和:1-(1/2)C(n,1)+(1/3)C(n,2)-.....+((-1)^n)/(n+1))C(n,n)=?

真真

回覆: 1

2020-06-15 8:05 pm

證明n+1必可整除C(2n,n)?

真真

回覆: 0

2020-06-10 11:22 pm

假設任兩人同一天生日的概率為1/365,若要使N人當中能找到6人都在同一天生日的概率不少於1/2,問N最少值為何?

真真

回覆: 1

2020-06-06 10:09 pm

太陽系模型系列一套九款包括太陽及八大行星,以每盒內含三款的形式發售,且同一盒款式隨機但不重複。若買方無法看到盒內所附款式,則平均而言至少買幾盒才可集齊一套九款?

真真

回覆: 1

2020-05-29 10:14 pm

擲硬幣的期望值問題?

真真

回覆: 2

2020-03-27 2:52 pm

函數f(x)=√(x+3)+√(1-x)的最大值和最小值為何?

真真

回覆: 1

2020-03-24 2:47 pm

三個正數x,y,z滿足x+y=xy和x+y+z=xyz,試求z的取值範圍?

真真

回覆: 1

2020-03-22 2:55 pm

求(√(1-x^2))/(x+1)的取值範圍?

真真

回覆: 1

2020-03-20 2:43 pm

若x≥1,y≥1,且(logx)^2+(logy)^2=log(10x^2)+log(10y^2),問log(xy)最大值為何?

真真

回覆: 1

2020-03-04 2:50 pm

已知x+y=4,問1/(x^2+1)+1/(y^2+1)之最大值為何?