如圖,一圓交三角形ABC於點A,D,F,G,E,而過點F的圓BDF的切線和過點G的圓CEG的切線交於T,若A和T不重合,證明AT//BC?

問題：
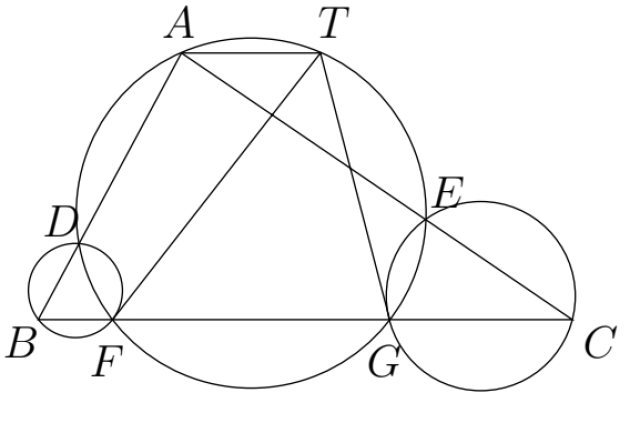
如圖，一圓交三角形 ABC 於點 A，D，F，G，E，而過點 F 的圓 BDF 的切線和過點 G 的圓 CEG 的切線交於 T，若 A 和 T 不重合，證明 AT//BC。

https://s.yimg.com/tr/i/3ea52c071c064a739fecb971dc0f5ee3_A.png
🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘
解答：
連 DF、EF 及 EG。

∠TFE
= ∠DFE - ∠DFT
= (180° - ∠BAC) - ∠ABC ...... ( 圓內接四邊形對角 及 交錯弓形的圓周角 )
= ∠ACB ...... ( 三角形內角和 )
= ∠TGE ...... ( 交錯弓形的圓周角 )
∴ F、G、E 及 T 四點共圓。 ...... ( 同弓形內的圓周角的逆定理 )
故 A、D、F、G、E 及 T 六點共圓。

∠TAC
= ∠TGE ...... ( 同弓形內的圓周角 )
= ∠ACB ...... ( 交錯弓形的圓周角 )
∴ AT//BC ...... ( 錯角相等 )
🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘
註：
同弓形內的圓周角的逆定理：
若 ∠TFE = ∠TGE，則 F、G、E 及 T 四點共圓。

證明：
https://s.yimg.com/tr/i/2b92f2d4792b4c0d92f3e8bcc121809f_A.png

假設 F 為圓 TGE 外的一點。記 F' 為 TF 與圓 TGE 的交點。連 F'E。
∠TFE + ∠FEF'
= ∠TGE + ∠FEF' ...... ( 已證 )
= ∠TF'E + ∠FEF' ...... ( 同弓形內的圓周角 )
= (∠TFE + ∠FEF') + ∠FEF' ...... ( 三角形外角 )
故 ∠FEF' = 0°，即 F 與 F' 重合，則 F 必為圓 TGE 上的一點。

假設 F 為圓 TGE 內的一點。延伸 TF 至 F'，使得 F' 為圓上的一點。連 F'E。
∠TF'E + ∠FEF'
= ∠TGE + ∠FEF' ...... ( 同弓形內的圓周角 )
= ∠TFE + ∠FEF' ...... ( 已證 )
= (∠TF'E + ∠FEF') + ∠FEF' ...... ( 三角形外角 )
故 ∠FEF' = 0°，即 F 與 F' 重合，則 F 必為圓 TGE 上的一點。

∴ F、G、E 及 T 四點共圓，即 T 一定在圓 ADFGE 上。
🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘