What is the shortest distance ?
2021-04-13 5:17 pm
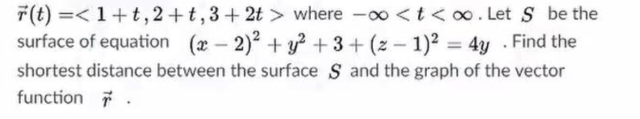
回答 (1)
2021-04-13 8:13 pm
✔ 最佳答案
曲線上一點 (1+t,2+t,3+2t) 到曲面(x-2)^2 + y^2 + 3 + (z-1)^2 = 4y
上一點之距離的平方是
(x-1-t)^2 + (y-2-t)^2 + (z-3-2t)^2
所以問題相當於
minimize (x-1-t)^2 + (y-2-t)^2 + (z-3-2t)^2
subject to (x-2)^2 + y^2 +3 + (z-1)^2 = 4y
限制條件改寫成 (x-2)^2 + (y-2)^2 + (z-1)^2 = 1.
這是問曲線至以 (2,2,1) 為球心之單位球面的最短距離.
固定曲線上一點,
點至球面的距離 = 點與球心距離 - 球之半徑
= √[(1+t-2)^2 + (2+t-2)^2 + (3+2t-1)^2] - 1
= √(6t^2+6t+5) - 1
= √[6(t+1/2)^2+7/2] - 1
距離最短發生在 t = -1/2 時, 最短距離 √(7/2) - 1.
收錄日期: 2021-05-04 00:41:42
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20210413091712AAHdB8J

