What is the maximum area of triangle ABC?
2021-04-13 5:15 pm
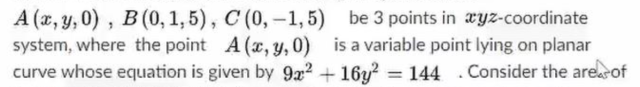
回答 (1)
2021-04-13 7:38 pm
✔ 最佳答案
三角形的底. BC 邊長為 2.從 A 到 B, C 連線之距離, 是 BC 線上一點 D
到 A 點連線段的長度, 其中 AD線 ⊥ BC 線.
D 點座標是 (0,t,5),
向量(x,y-t,-5) ⊥ 向量(0,2,0)
所以 t = y, 即 D 座標 (0,y,5). 所以
AD = √[(x-0)^2+(y-y)^2+(0-5)^2]
= √(x^2+5^2)
三角形面積 = 1/2 × 底 × 高.
所以, 面積最大相當於 AD長 最大, 相當於
x^2+25 最大, 相當於 x^2 最大.
因點 A 在 xy-平面上, 滿足
9x^2 + 16y^2 = 144
所以 x^2 最大值是 144/9 = 16.
所以 AD 最大長度是 √41,
三角形 ABC 最大面積 √41.
收錄日期: 2021-05-04 00:39:37
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20210413091519AA0GhLC

