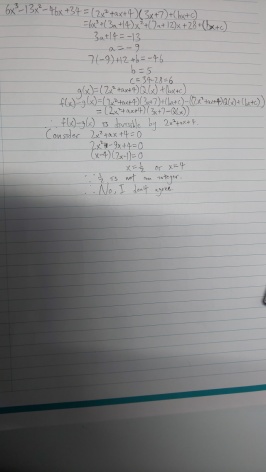回應管理員:
我見到自己個名 (8:50) 係排名榜, 仲見到 no3lunch 同 TOMING88 知識長:
https://www.youtube.com/watch?v=gxqNY1FS4Hw
唔知大家知唔知 知識家 將會結束?
老怪物師父? 管理員? SC147? 其他高手?
= = = = = = = = = =
回覆老怪物師父:
香港這一邊的高中課程沒有教 number theory, 所以學生沒有同餘 modulus 的概念。
相信本題設定quadratic是讓學生能夠做到因式分解。
知識家一再改版,甚至即將結業。
感謝各位十多年來對於知識的分享並交流。
我最欣賞是初期之中期的版本,不但有知識豆升級制和問答環節,也有意見欄和專題發帖作文章分享。也有贊助點數、投票、點評等等的環節,比較似一個論壇。大家可以交流切磋,也有機會「認識」各位會員。
之前另一個我回應smile的發問帖我提及公司的賣盤問題不止被隱藏,而且整個帖被刪除。可能有人審核內文。
回應smile:
如果移到日本區發問,可能當地的受眾或相關管理員會覺得怪異,因為看不懂中文。
(a)
f(x) ≡ (2x² + ax + 4)(3x + 7) + (bx + c)
6x³ - 13x² - 46x + 34 ≡ (2x² + ax + 4)(3x + 7) + (bx + c)
Put x = 0, 34 = 28 + c ⇒ c = 6
Put x = 1, -19 = 60 + 10a + b + 6 ⇒ 10a + b = -85 ...(1)
Comparing coefficient of x: -46 = 7a + 12 + b ⇒ 7a + b = -58 ...(2)
(1) - (2): 3a = -27 ⇒ a = -9, b = 5
a = -9
(b) (i)
When the quadratic polynomial g(x) [degree 2] is divided by (2x² + ax + 4) [degree 2], let the quotient be Q (a constant, degree = 2 - 2 = 0), then
g(x) = (2x² + ax + 4)Q + (bx + c) ...(3)
Also note that
f(x) ≡ (2x² + ax + 4)(3x + 7) + (bx + c) ... (4)
(4) - (3) gives f(x) - g(x) = (2x² + ax + 4)(3x + 7 - Q)
Because (3x + 7 - Q) is a polynomial, f(x) - g(x) is divisible by (2x² + ax + 4).
(b) (ii)
For f(x) - g(x) = 0,
(2x² + ax + 4)(3x + 7 - Q) = 0
(2x² - 9x + 4)(3x + 7 - Q) = 0
One of the roots is (Q - 7)/3 which may not be an integer.
Therefore, the claim is not agreed.