a. Write the balanced equation representing Ir-192 undergoing beta decay and it accompanying rate law
b. Determine the rate constant k for this reaction
c. How many grams of a 50.0g sample of Iridium-192 remain after 5 years
The decay of Iridium-192 which is a first-order reaction with a half-life of 74 days?
2021-03-24 8:42 am
回答 (1)
2021-03-24 10:42 am
✔ 最佳答案
a.The balanced equation is shown at the bottom.
The rate equation: Rate = k A,
where A is the amount of iridium-192.
====
b.
Rate constant, k = ln(2)/t½ = ln(2)/(74 days) = 0.009367 day⁻¹ ≈ 0.00937 day⁻¹
====
c.
No. of half-lives = (5 × 365.25 days) / (74 days) = 24.68
Mass after 5 years = (50.0 g) × (1/2)²⁴·⁶⁸ = 1.86 × 10⁻⁶ g
OR:
Time taken, t = 5 × 365.25 days = 1826.25 days
Mass after 5 years, A = Aₒ e⁻ᵏᵗ = (50.0 g) × e⁻⁰·⁰⁰⁹³⁶⁷ˣ¹⁸²⁶·²⁵ = 1.86 × 10⁻⁶ g
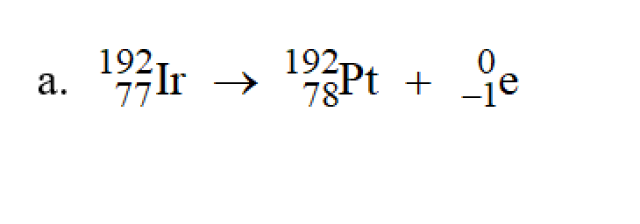
收錄日期: 2021-04-23 23:07:34
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20210324004258AAAeBnM

