Would you please help to answer the following question for me ?
2021-03-06 8:36 pm
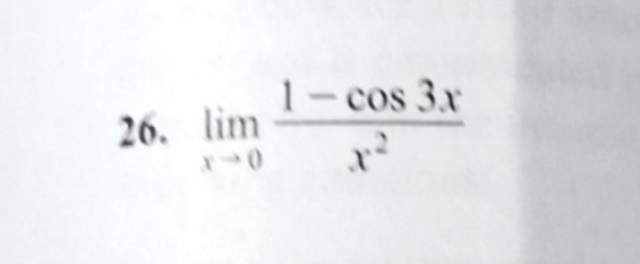
回答 (1)
2021-03-07 12:51 am
✔ 最佳答案
因為是 0/0 不定式, 可用 l'Hospital's rule:當 x → 0, (1-cos(3x))/x^2 ~ 3sin(3x)/(2x)
lim_{x→0} (3sin(3x))/(2x)
= (3/2) lim+(x→0} sin(3x)/x
= (3/2) (d/dx) sin(3x)|_{x=0}
= (3/2) 3cos(3x)|_{x=0}
= 9/2
∴ lim_{x→0} (1-cos(3x))/x^2 = 9/2
亦可不用 l'Hospital's rule 而用更基礎的公式:
(1-cos(3x))/x^2 = 2sin^2(3x/2)/x^2
= 2 (sin(3x/2)/x)^2
因 x→0 時,
sin(3x/2)/x = (3/2) sin(3x/2)/(3x/2) → 3/2
故得
lim_{x→0} (1-cos(3x))/x^2 = 2(3/2)^2 = 9/2
收錄日期: 2021-05-04 00:38:38
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20210306123633AAvgeOa

