高二柯西不等式,這題不知怎麼解。?
2021-03-02 8:44 pm
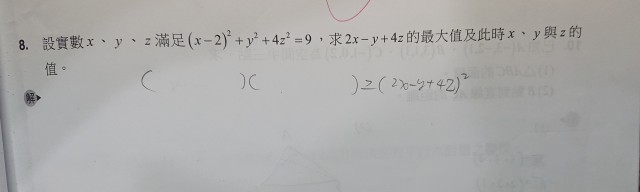
回答 (2)
2021-03-03 9:05 am
✔ 最佳答案
[(x-2)^2+y^2+(2z)^2] × [2^2+(-1)^2+2^2] ≧ [2(x-2)+(-1)y+2(2z)]^2
= (2x-y+4z-4)^2不等式之等號成立的充要條件是
x-2 : 2 = y : -1 = 2z : 2
即
x = 2 + 2t, y = -t, z = t
由 (x-2)^2+y^2+4z^2 = 9 得 t = ±1
故
x = 4, y = -1, z = 1 或 x = 0, y = 1, z = -1.
此兩解使等式成立, 也就是 (2x-y+4z-4)^2 達最大,
分別對應 2x-y+4z-4 之最大與最小.
不等式兩邊
9 × 9 ≧ (2x-y+4z-4)^2
故
-9 ≦ 2x-y+4z-4 ≦ 9
即
-5 ≦ 2x-y+4z ≦ 13
最大值 13, 發生於 x = 4, y = -1, z = 1.
2021-03-02 9:50 pm
列兩個式,先把前一個公式的數值算出來,再求後面公式的數值,再看兩個數列是需要相乘還是互加,然後再除盡
收錄日期: 2021-05-04 02:32:40
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20210302124401AA6PmOR


