數學題 有沒有人會🧎🏽‍♂️🧎🏽‍♂️🙏急?

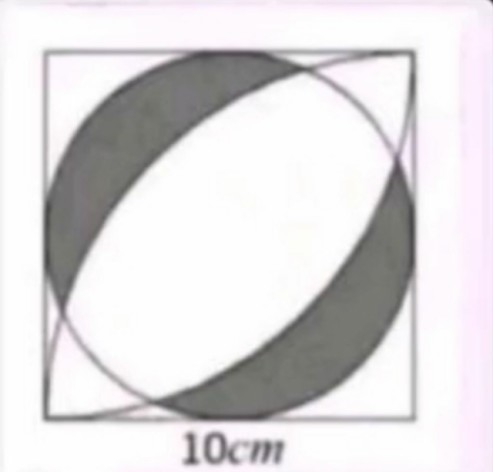
□ABCD 邊長 a 的正方形. 內切圓圓心 O, 半徑 a/2.
分別以 A, C 為圚心, 以 a 為半徑作圓弧, 交圓 O 於
P. Q; R, S. 欲求 PQ 弧之外, 圓 O 內, 與 RS 弧外
圓 O 內之區域面積.

BD 對角線將圖分為兩半(O是BD線段中點), 算出一半之
面積再乘以2即是結果.

連 PQ, 則陰影月形之面積為圓 O 上 PQ 弓形減去 C 為
圓心之 PQ 弓形. 因此,必須算出 ∠POQ 與 ∠PCQ.

CP = CQ = a, OP = OQ = a/2, OC = (√2/2)a.
用餘弦定律可算出
  ∠PCO = ∠QCO = acos(5√2/8)
  ∠CPQ = ∠CQO = acos(3/4)
∴ ∠PCQ = 2 acos(5√2/8)
   ∠POQ = 2(acos(5√2/8)+acos(3/4)) = 2 acos(√2/4)

PQ 弦長度是
   2a sin(∠PCO) = (√14/4)a = 2(a/2) sin(∠PCO+∠CPQ)
O, C 至 PQ 弦的垂直距離分別是 (√2/8)a , (5√2/8)a

基於圓 O 之 PQ 扇形區域面積是
   (a/2)^2(∠POQ/2) = a^2 acos(√2/4)/4
△OPQ 面積是
   (1/2)．(√14/4)a．(√2/8)a = (√7/32)a^2
故基於圓 O 之 PQ 弓形區域面積是
   (acos(√2/4)/4 - √7/32) a^2

類似地, 計算基於以 C 為圓心半徑 a 之 PQ 弓形區域
面積是
   (acos(5√2/8) - 5√7/32) a^2

所以, PQ 月形區域面積是
   (acos(√2/4)/4 - acos(5√2/8) + √7/8) a^2
     ≒ (0.3023573007-0.4866949551+0.3307189139)a^2
     ≒ 14.638126cm^2
而 RS 月形區域面積同 PQ 月形區域, 故整個圖形陰影
部分面積是 14.638126cm^2 × 2 = 29.276252cm^2.