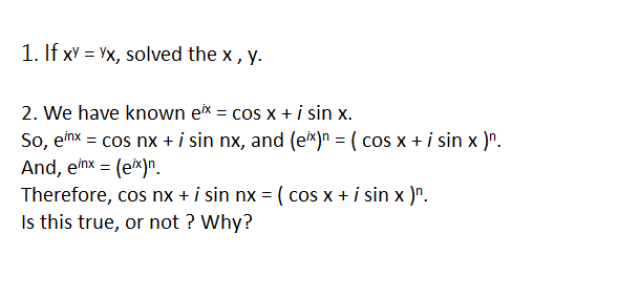✔ 最佳答案
x^y = x^(x^....^x) 括弧內是 y-1 個 x ?
依題意, 則 y 是正整數.
若 y = 1, x^1 = x 成立.
設 y = n > 1,
若 x = 1, 則 x^y = 1 = x^(x^...^x), 等式成立.
設 y = n > 1 且 x ≠ 1.
若 x = -1, 則 (-1)^(-1) = 1/(-1)^1 = -1
而 n 為奇數時 (-1)^n = -1, 故 x^y = x^(x^...^x) 成立.
允許 x < 0 時, x 必須是特定有理數才能適當定義
(即使在複數系能定義, 也涉及多值問題, 因此不考慮).
因此假設 x 非負.
但又涉及 0^0 定義問題, 故除 x = -1 特例外,
假設 x > 0, 並設 x ≠1.
故 x^y = x^(x^...^x) 等價於
y = x^...^x, 右方為 y-1 個 x 構成.
故 y 取不同正整數得不同的一元方程式, 如
y = 2 = x
y = 3 = x^x
y = 4 = x^x^x = x^(x^x)
y = 5 = x^x^x^x = x^(x^(x^x))
由於 x^x...^x 在 [1,∞) 是映成 [1,∞) 的嚴格增函數,
所以上列諸方程式都有唯一解.
結論:
限制 y 為正整數.
設 x^y = x^...^x 中右式是指 y 個 x 的連續乘冪型,
則 y = 1 時是 x^1 = x, 對任意 x 都成立.
x = -1 時, y 取奇數等式皆成立;
x = 1 時 y 為任何正整數;
x > 0 且 x ≠ 1 時, 對任意大於 1 的 y, 恰有一 x > 1
滿足 x^y = x^...^x.
圖像中第一題, 等式右邊的運算我孤陋寡聞未曾學過.
第2題, 由複數乘法、兩角和之 sin, cos 公式、配合數學歸納法,
易證
cos(nx) + i sin(nx) = (cos x + i sin x)^n
對任意正整數 n 成立.