數學問題急急急???求大大幫忙!!?
2021-01-23 1:53 pm
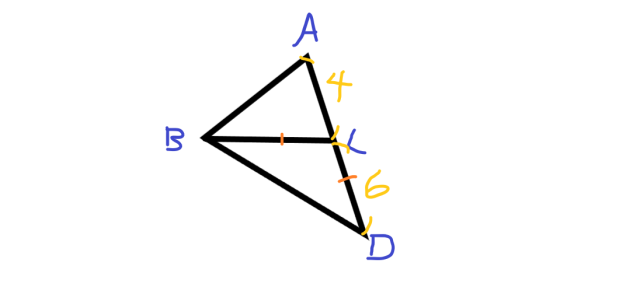
△ABD 中,C 為AD 上一點,若∠ACB=2∠ABC,且BC = CD =6, AC =4,. 則AB 的長為何?
回答 (1)
2021-01-24 12:05 am
問題:
△ABD 中,C 為 AD 上一點,若 ∠ACB = 2∠ABC,且 BC = CD = 6,AC = 4,則 AB 的長為何?
https://s.yimg.com/tr/i/caa304b984094980bc3f3c607a1ab588_A.png
🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘
解答:
方法一:
https://s.yimg.com/tr/i/81c860d1d87147579b502ab3d5e815c1_A.png
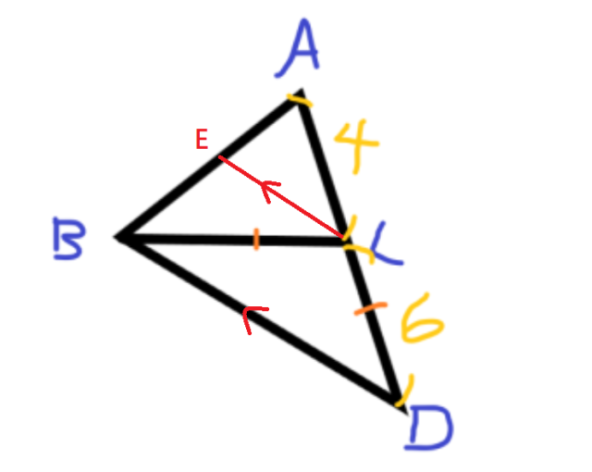
設 E 為 AB 上的線,使得 EC//BD。
∵ ΔABD ~ ΔAEC
BD:EC = 5:2 及 BE:EA = 6:4 = 3:2
∵ EC//BD
∠EBC = 0.5 ∠ACB = ∠CBD = ∠ECB
∴ ΔBCE ~ ΔBDC,即 BE = CE
BE×BD = BC²
BE ( 5EC/2 ) = 36
BE = √(36×2/5) = √(72/5) = (6/5)√(9 + 1)
AB = (5/3) (6/5)√(9 + 1) = 2√(9 + 1)
方法二:
https://s.yimg.com/tr/i/5ae5098cf72d4f0abfa090c792729809_A.png
延長 BC 至 E,使得 EC = 4。
設 F 為 BD 上的點,使得 AF⊥BD。
∵ ∠ABC = ∠DBC
∴ AB:BD = 4:6 = 2:3
∵ ΔCBD ~ ΔCEA
∠CEA = (∠CBD + ∠CDB)/2 = 0.5 ∠ACB = ∠ABC
∴ AB = AE
∵ ΔCBD ~ ΔCEA 及 ΔACB ≅ ΔECD
∴ ABCE 為等腰梯形,即 AE = AB = ED
AB² - BF² = AD² - DF²
AB² - [(BD - AE)/2]² = (9 + 1)² - [(BD - AE)/2 + AE]²
AB² - [(3AB/2 - AB)/2]² = (9 + 1)² - [(3AB/2 - AB)/2 + AB]²
AB = 2√(9 + 1)
🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘
△ABD 中,C 為 AD 上一點,若 ∠ACB = 2∠ABC,且 BC = CD = 6,AC = 4,則 AB 的長為何?
https://s.yimg.com/tr/i/caa304b984094980bc3f3c607a1ab588_A.png
🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘
解答:
方法一:
https://s.yimg.com/tr/i/81c860d1d87147579b502ab3d5e815c1_A.png
設 E 為 AB 上的線,使得 EC//BD。
∵ ΔABD ~ ΔAEC
BD:EC = 5:2 及 BE:EA = 6:4 = 3:2
∵ EC//BD
∠EBC = 0.5 ∠ACB = ∠CBD = ∠ECB
∴ ΔBCE ~ ΔBDC,即 BE = CE
BE×BD = BC²
BE ( 5EC/2 ) = 36
BE = √(36×2/5) = √(72/5) = (6/5)√(9 + 1)
AB = (5/3) (6/5)√(9 + 1) = 2√(9 + 1)
方法二:
https://s.yimg.com/tr/i/5ae5098cf72d4f0abfa090c792729809_A.png
延長 BC 至 E,使得 EC = 4。
設 F 為 BD 上的點,使得 AF⊥BD。
∵ ∠ABC = ∠DBC
∴ AB:BD = 4:6 = 2:3
∵ ΔCBD ~ ΔCEA
∠CEA = (∠CBD + ∠CDB)/2 = 0.5 ∠ACB = ∠ABC
∴ AB = AE
∵ ΔCBD ~ ΔCEA 及 ΔACB ≅ ΔECD
∴ ABCE 為等腰梯形,即 AE = AB = ED
AB² - BF² = AD² - DF²
AB² - [(BD - AE)/2]² = (9 + 1)² - [(BD - AE)/2 + AE]²
AB² - [(3AB/2 - AB)/2]² = (9 + 1)² - [(3AB/2 - AB)/2 + AB]²
AB = 2√(9 + 1)
🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘🔘
收錄日期: 2021-04-24 08:11:36
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20210123055357AAaGFxk
