求指數方程過程,急!?
2021-01-20 11:13 pm
已知答案r=2%,求詳細過程是如何得出答案的,謝謝。
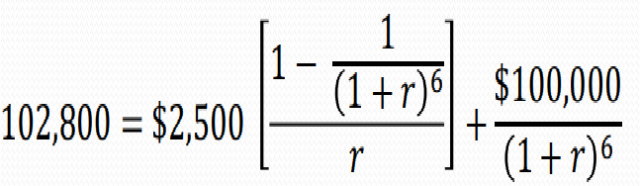
回答 (1)
2021-01-21 1:03 am
✔ 最佳答案
(為免被隱, 部分0改以o代替)(1) 初步近似法
1o28oo = 25oo{[1-1/(1+r)^6]/r} +1ooooo/(1+r)^6
= 25oo{[1-(1+r)^(-6)]/r} + 1ooooo(1+r)^(-6)
≒ 25oo{[1-(1-6r+6.7/2 r^2 - 6.7.8/6 r^3)]/r}
+ 1ooooo(1-6r+6.7/2 r^2)
= 25oo(6-21r+56r^2) + 1ooooo(1-6r+21r^2)
= 115000 - 652500r + 2240000r^2
一階近似:
13000 ≒ 652500r
∴ r ≒ 13000/652500 = 26/1305 ≒ 1.992%
二階近似:
13000 - 652500r + 2240000r^2 ≒ 0
∴ r ≒ 0.1456473214 ± 0.1241352924
考慮實務, 又參考一階近似, 取較小正根, 得
r ≒ 2.151%
(2) 試算修正
E(r) = 25oo{[1-1/(1+r)^6]/r} +1ooooo/(1+r)^6 - 1o28oo
r = 1.992%, E(r) ≒ 46 > 0;
r = 2.151%, E(r) ≒ -855 < 0
正確 r 值介於 1.992% 與 2.151 之間.
可用線性插補得 r 之較精確近似:
(2.151-1.992)*[46/(46+855)]+1.992 ≒ 2
r = 2% 是插補近似解. 代入誤差公式 E(r) 得
E(r) ≒ 0 故最後取值 r = 2%
收錄日期: 2021-05-04 02:31:40
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20210120151315AAgtCkW

