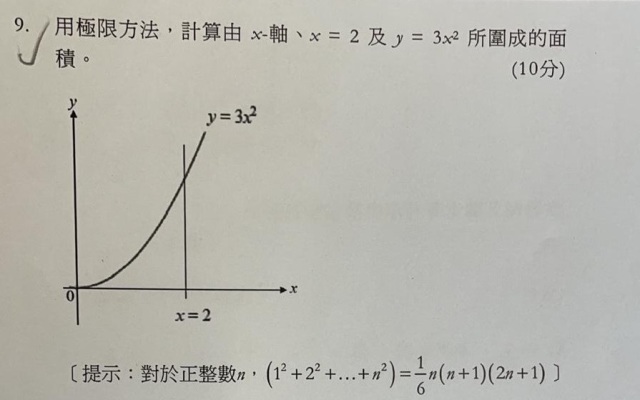
Maths-M2 積分求面積?

其實就是計算  ∫_[0 to 2] 3x^2 dx  而已.

不過, 題目說要用 "極限" 方法, 也就是要用
黎曼和. 取點 2n/, 4/n, ..., (2n)/n. 則
    Σ_{k = 1 to n} 3[2(k-1)/n]^2．(2/n)
      ≦  ∫_[0 to 2] 3x^2 dx = A
      ≦ Σ_{k = 1 to n} 3(2k/n)^2．(2/n)
即 
    Σ_{i = 0 to n-1} 12i^2/n^2．(2/n)
      ≦ A ≦ Σ_{k = 1 to n} 12k^2/n^2．(2/n)
即 
    (24/n^3)Σ_{i = 0 to n-1} i^2
       ≦ A ≦  (24/n^3)Σ_{k = 1 to n} k^2

把平方和公式套用上去, 令 n→∞ 取極限,
即得 A 之值.