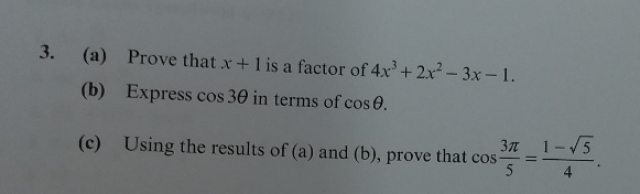(a) is (x+1)(4x^2 - 2x -1)
(b) 4cos^3 (theta) - 3cos(theta)
(c) if let x=cos(pi/5), then cos(3theta) = 4cos^3(pi/5) - 3cos(pi/5)=4x^3 - 3x
But then how to proceed? where does the factor x+1 come in?
更新1:
Hi, Gong, yes of course.