✔ 最佳答案
2021/01/13:
昨天看到你在回答區問的, 我就補充了.
(1/2)tan(θ)(1+tan^2(θ/2))/(tan(θ)+tan(θ/2))
= (1/2)tan(θ)sec^2(θ/2)/(tan(θ)+tan(θ/2))
= (1/2)(1/cos^2(θ/2))/(1+tan(θ/2)/tan(θ))
= (1/2)/(cos^2(θ/2)+cos^2(θ/2)tan(θ/2)/tan(θ))
請再看看還有哪裡寫得不夠清楚.
=============================
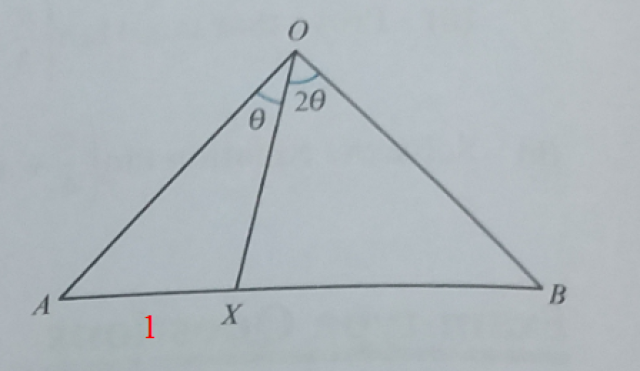
作 線段OC⊥AB邊 於 C.
則 ∠COX = θ/2,
∴ CX/OX = sin(θ/2)
OC/OX = cos(θ/2)
(1/2)/OA = sin(3θ/2)
OC/OA = cos(3θ/2)
∴ OC = cot(3θ/2)/2
OX = cot(3θ/2)/(2cos(θ/2))
CX = cot(3θ/2)tan(θ/2)/2
AX = 1/2 - cot(3θ/2)tan(θ/2)/2
= (1/2)(1-tan(θ/2)/tan(3θ/2))
= (1/2)[1-tan(θ/2)(1-tan(θ)tan(θ/2))/(tan(θ)+tan(θ/2))]
= (1/2)tan(θ)(1+tan^2(θ/2))/(tan(θ)+tan(θ/2))
= (1/2)tan(θ)sec^2(θ/2)/(tan(θ)+tan(θ/2))
= (1/2)(1/cos^2(θ/2))/(1+tan(θ/2)/tan(θ))
= (1/2)/(cos^2(θ/2)+cos^2(θ/2)tan(θ/2)/tan(θ))
= (1/2)/(cos^2(θ/2)+sin(θ/2)cos(θ/2)/tan(θ))
= (1/2)/[(1+cos(θ))/2 +(1/2)sin(θ)/tan(θ)]
= 1/(1+2cos(θ))