Please answer the following question, thank you?
2021-01-07 11:38 pm
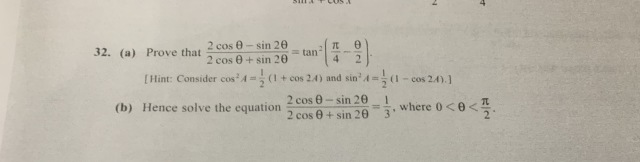
回答 (1)
2021-01-09 6:25 pm
✔ 最佳答案
(a)Use the hint:
sin²A = (1/2) (1 - cos 2A) ...[1]
cos²A = (1/2) (1 + cos 2A) ...[2]
[1]÷[2] gives
tan²A = (1 - cos 2A)/(1 + cos 2A)
Put A = π/4 - θ/2,
tan²(π/4 - θ/2)
= [1 - cos(π/2 - θ)]/[1 + cos(π/2 - θ)]
= (1 - sinθ)/(1 + sinθ)
= (cosθ - sinθcosθ)/(cosθ + sinθcosθ)
= (2cosθ - 2sinθcosθ)/(2cosθ + 2sinθcosθ)
= [2cosθ - sin(2θ)]/[2cosθ + sin(2θ)]
(b)
Note that for 0 < θ < π/2,
we have 0 < θ/2 < π/4,
and -π/4 < -θ/2 < 0,
i.e. 0 < π/4 - θ/2 < π/4.
Using the result of (a), the equation is
tan²(π/4 - θ/2) = 1/3
tan(π/4 - θ/2) = 1/√3 or -1/√3 (rejected for 0 < π/4 - θ/2 < π/4)
π/4 - θ/2 = π/6
θ/2 = π/4 - π/6
θ/2 = π/12
θ = π/6
收錄日期: 2021-04-23 23:44:11
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20210107153835AA8CkyB
