數學問題急急急???求大大幫忙!!?
2021-01-07 10:21 pm
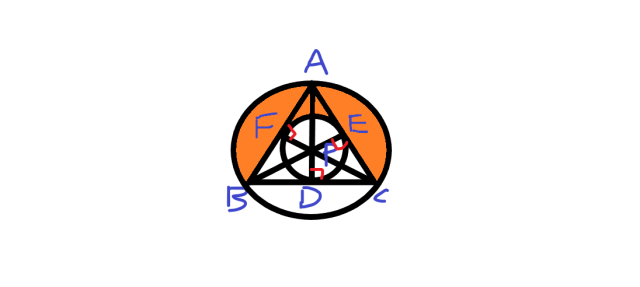
正三角形ABC中,P點為中線BE、AD、CF的交點,BC=6,則塗色面積、周長分別為何?
回答 (1)
2021-01-08 7:42 am
✔ 最佳答案
正三角形其內切圓半徑 (EP) 是中線也是角平分線長 BE 的 1/3, 而 BE 是邊長 (BC) 的√3/2 (△BCE
是 30-60-90 的直角三角形); 外接圓半徑 BP 則是
BE 的 2/3. 因正三角形 △ABC 邊長為 6, 所以:
(1) 高 AD = BE = (√3/2).6 = 3√3, 面積
(1/2)(6)(3√3) = 9√3;
(2) 內切圓半徑 PE = 3√3.(1/3) = √3;
(3) 外接圓半徑 PB = 2√3.
大弓形面積是 1/3 大圓面積 - 1/3 三角形面積
(△PAB 面積是 △ABC 的 1/3);
小弓形面積是 1/3 三角形面積 - 1/3 小圓面積
(□ARPF 面積是 △ABC 的 1/3).
所以, 塗色區域面積:
A = [π(2√3)^2.(1/3) - (9√3).(1/3)].2
+[(9√3).(1/3) - π(√3)^2.(1/3)]
= 2(4π - 3√3) + (3√3 - π)
= 7π - 3√3.
塗色區域周長
= 弧AB長 + 弧AC長 + 弧EF長 + BF + CE
= (2/3)(大圓周長) + (1/3)(小圓周長) + 2(6/2)
= (2/3)(2π.2√3) + (1/3)(2π.√3) + 6
= 1o√3π/3 + 6 = 1oπ/√3 + 6
收錄日期: 2021-05-04 02:32:09
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20210107142115AAPvn9u

