這道題目如何計算和驗算呢?
2021-01-07 3:15 pm
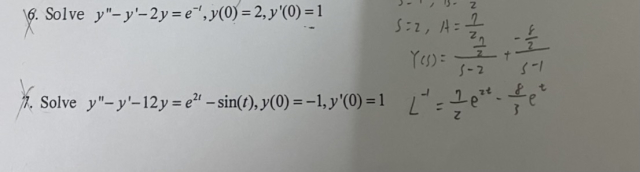
回答 (2)
2021-01-09 2:31 pm
你需要使用操作計算機,可以研讀參考書籍:計算機概論。
2021-01-08 8:30 am
常係數二階微分方程
y" + by' + cy = g(t)
其通解可寫成 y = y_h + y_p,
y_h 是對應的齊次方程 y" + by' + cy = 0 的通解;
y_p 是原方程式任一(特)解.
而尋找特解有多種方法, 例如待定係數法, 是已
知特解形式, 只是係數待定. 當然工數裡面可能
愛用 Laplace transform 或 Fourier transform.
Laplace transform 不過是把原微方化成 Laplace
transform 之方程式, 求出 y 之 LT 後再找出對應
的函數. Fourier transform 也一樣, 只不過 FT 有
對應的 inverse FT, 而且它和 FT 幾乎可說是一樣
的.
且說說待定係數法. 此法適合 g(t) 是多項式、簡
單指數 (e^(kt)), 正餘弦.
如第一個方程式 g(t) = e^(-t), 則 y_p 本來應該
是 Ae^(-t), 但因 y_h 部分有 e^(-t), 所以 y_p 在
e^(-t) 之前加個 t, 成為 y_p = Ate^(-t).
如第二個方程式 g(x) = e^(2t) - sin(t), 則
y_p = Ae^(2t) + B1 cos(t) + B2 sin(t)
即 g(t) 中的正弦或餘弦對應特解中的正餘弦組
合. 將此特解代入原方程式即能解出諸係數.
通解中的 "任意常數" 在代入初值條件 y(0), y'(0)
後確定, 而不再 "任意".
至於解之驗算, 就是把解代入原方程式看符不符
合. 另外就是 y_h 中 "任意常數" 個數是與方程式
階數一致的, 如圖中兩方程式都是二階, 就會有兩
個 "任意常數", 也就是說 y_h 是由兩個線性獨立
的指數函數之線性組合構成.
圖中兩方程式的特性方程式都可以簡單因式分解
成一次式乘積, 如第一題, r^2 - r - 2 = 0 因式分解
成 (r+1)(r-2) = 0, 因此, 也可以用一階方程的解法
逐步得出 y 之解.
y" + by' + cy = g(t)
其通解可寫成 y = y_h + y_p,
y_h 是對應的齊次方程 y" + by' + cy = 0 的通解;
y_p 是原方程式任一(特)解.
而尋找特解有多種方法, 例如待定係數法, 是已
知特解形式, 只是係數待定. 當然工數裡面可能
愛用 Laplace transform 或 Fourier transform.
Laplace transform 不過是把原微方化成 Laplace
transform 之方程式, 求出 y 之 LT 後再找出對應
的函數. Fourier transform 也一樣, 只不過 FT 有
對應的 inverse FT, 而且它和 FT 幾乎可說是一樣
的.
且說說待定係數法. 此法適合 g(t) 是多項式、簡
單指數 (e^(kt)), 正餘弦.
如第一個方程式 g(t) = e^(-t), 則 y_p 本來應該
是 Ae^(-t), 但因 y_h 部分有 e^(-t), 所以 y_p 在
e^(-t) 之前加個 t, 成為 y_p = Ate^(-t).
如第二個方程式 g(x) = e^(2t) - sin(t), 則
y_p = Ae^(2t) + B1 cos(t) + B2 sin(t)
即 g(t) 中的正弦或餘弦對應特解中的正餘弦組
合. 將此特解代入原方程式即能解出諸係數.
通解中的 "任意常數" 在代入初值條件 y(0), y'(0)
後確定, 而不再 "任意".
至於解之驗算, 就是把解代入原方程式看符不符
合. 另外就是 y_h 中 "任意常數" 個數是與方程式
階數一致的, 如圖中兩方程式都是二階, 就會有兩
個 "任意常數", 也就是說 y_h 是由兩個線性獨立
的指數函數之線性組合構成.
圖中兩方程式的特性方程式都可以簡單因式分解
成一次式乘積, 如第一題, r^2 - r - 2 = 0 因式分解
成 (r+1)(r-2) = 0, 因此, 也可以用一階方程的解法
逐步得出 y 之解.
收錄日期: 2021-05-04 02:37:20
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20210107071500AASpv3M


