Please answer the following question?
2021-01-06 10:22 pm
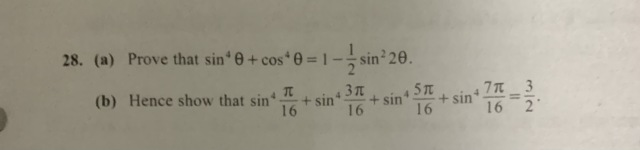
回答 (1)
2021-01-09 5:47 pm
✔ 最佳答案
(a)LHS
= sin⁴θ + cos⁴θ
= sin⁴θ + 2sin²θcos²θ + cos⁴θ - 2sin²θcos²θ
= (sin²θ + cos²θ)² - (1/2) 2²sin²θcos²θ
= 1² - (1/2) (2sinθcosθ)²
= 1 - (1/2) sin²(2θ)
= RHS
(b)
sin⁴(π/16) + sin⁴(3π/16) + sin⁴(5π/16) + sin⁴(7π/16)
= sin⁴(π/16) + sin⁴(3π/16) + cos⁴(π/2 - 5π/16) + cos⁴(π/2 - 7π/16)
= sin⁴(π/16) + sin⁴(3π/16) + cos⁴(3π/16) + cos⁴(π/16)
= sin⁴(π/16) + cos⁴(π/16) + sin⁴(3π/16) + cos⁴(3π/16)
= [1 - (1/2) sin²(π/8)] + [1 - (1/2) sin²(3π/8)] (by (a))
= [1 - (1/2) sin²(π/8)] + [1 - (1/2) cos²(π/2 - 3π/8)]
= [1 - (1/2) sin²(π/8)] + [1 - (1/2) cos²(π/8)]
= 1 + 1 - (1/2) [sin²(π/8) + cos²(π/8)]
= 2 - (1/2) (1)
= 2 - 1/2
= 3/2
收錄日期: 2021-04-23 23:47:53
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20210106142216AAG8cOG
