Maths problem: how to do, thanks.?

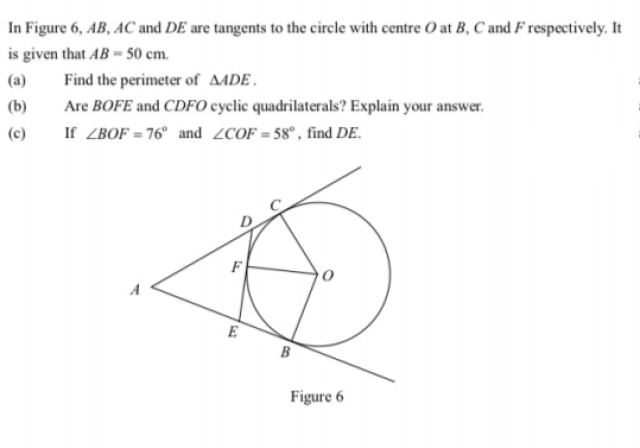
AB = AC = 50cm

設 DF = x, EF = y
則 DC = DF = x, EB = EF = y.

AE + AD + DE = AE + AD + x + y
    = AE + EB + AD + DC
    = AB + AC
    = 2AB = 1oocm

因為 OC⊥DC, OB⊥EB, OF⊥DE,
所以 □BOFE, □CDFO 各是相對兩內角互補,
所以它們都是圓內接四邊形.

設圓O 半徑 r, 則
DF = x = r．tan(∠COF/2)
EF = y = r．tan(∠BOF/2)
AB = r．tan((∠BOF+∠COF)/2)
∴ 50 = r．tan((76°+58°)/2)
   r = 50/tan(67°)
∴ DF = 50tan(29°)/tan(67°)
   EF = 50tan(38°)/tan(67°)
   DE = 50(tan(29°)+tan(38°))/tan(29°+38°)
      = 50(1-tan(29°)tan(38°))
      = 28.346(cm)

Thanks, 我看完終於明白了.