Maths problem: how to do, thanks?

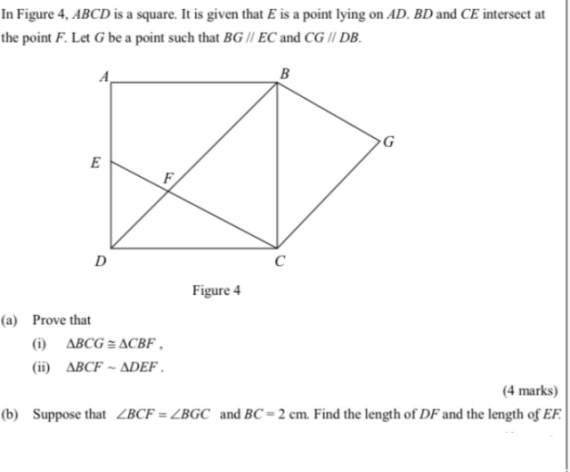
BG//FC, CG//FB
∴ □BFCG 是平行四邊形, 而 BG線段是其對角線.
∴ △BCG 全等於 △CBF
   (∠GBC = ∠FCB, ∠GCB = ∠FBC, BC邊 共用)

∠EFD = ∠CFB, ∠EDF = ∠CBF, ∠DEF = ∠BCF
∴ △BCF ～ △DEF

∠CBG = ∠BCF = ∠BGC
∴ CB = CG = BF
△DEF ～ △BCF 全等於 △CBG
∴ DE : DF : EF = CB : CG : BG = BC : BF : CF
BC = 2
∴ BF = 2
DF = DB - BF = (2√2 - 2)

∠CBF = 45°
CF = √{(BC)^2+(BF)^2-2(BC)(BF)cos45°} = 2√(2-√2)
EF = CF(DF/BF) = 2√(2-√2) (2√2-2)/2
   = 2√(4-2√2) - 2√(2-√2) = √(40-28√2)