Maths: how to do, thanks. I don't know how to do (b).?
回答 (2)
2021-01-03 6:17 pm
✔ 最佳答案
(a)f(x)=2x^3+ax^2+7x-9x=1f(1)=00=2+a+7-9a=0f(x)=2x^3+7x-9(bi)Area of OPQR=m(4m^2 +14)=4m^3+14m(bii)18=4m^3+14m2m^3+7m-9=0m=1
I agree
2021-01-03 5:50 pm
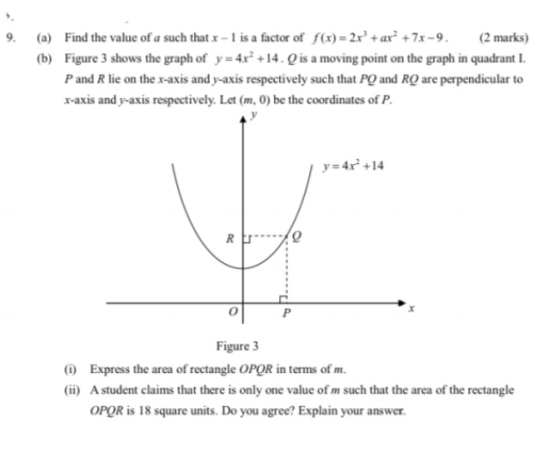
y = 4x^2 + 14
x = m ==> y = 4m^2+14
∴ P = (m,0), Q = (m,4m^2+14), R = (0,4m^2+14)
□OPQR 高 4m^2+14, 底 m,
面積 = m(4m^2+14)
m(4m^2+14) = 18
<==> 4m^3+14m-18 = 0
此3階方程式恰有一正根, 理由:
(1) 根據笛卡爾的符號律, 因方程式係數一次變號,
所以恰一正根.
(2) 用微積分方法, 上列方程式左邊對 m 做微分,
是一恆正函數 (12m^2+14), 所以方程式恰一實
根. 而用勘根定理可確定此根為正根.
x = m ==> y = 4m^2+14
∴ P = (m,0), Q = (m,4m^2+14), R = (0,4m^2+14)
□OPQR 高 4m^2+14, 底 m,
面積 = m(4m^2+14)
m(4m^2+14) = 18
<==> 4m^3+14m-18 = 0
此3階方程式恰有一正根, 理由:
(1) 根據笛卡爾的符號律, 因方程式係數一次變號,
所以恰一正根.
(2) 用微積分方法, 上列方程式左邊對 m 做微分,
是一恆正函數 (12m^2+14), 所以方程式恰一實
根. 而用勘根定理可確定此根為正根.
收錄日期: 2021-04-24 08:08:58
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20210103003148AANNeL8