我是用圓周長從z=R積到z=-R
但是不知道為什麼跟答案不一樣
請問球殼表面積積分?
2020-12-06 6:10 pm
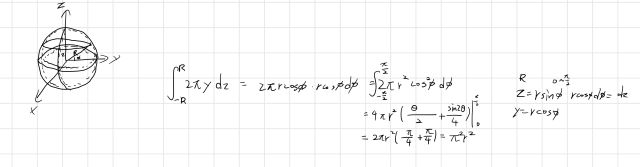
回答 (2)
2020-12-06 7:45 pm
Q: 我沒辦法理解你怎麼用圓錐切的
A:
還是先用 圓 x^2 + y^2 = R^2 來說吧.
從 y 到 y+dy, 圓 x^2 + y^2 = R^2 是不是被切出
左右兩段弧:
╭ ╮
把上下底分別連上, 是不是近似一個等腰梯形?
如果 y 變成 z, 圓方程式改成 x^2 + z^2 = R^2
繞 z 軸轉半圈, 不就是球 x^2 + y^2 + z^2 = R^2
了嗎? 而上述 "梯形" 旋轉後不就是一個圓錐台?
=====================================
首先, ∫_[-R,R] 2πy dz 這式就有點問題.
先不談求面積, 看圓周長, 如果用
∫_[-R,R] 2 dy
能算出圓周長嗎? 不! 當 y 變為 y+dy 時,
圓 x^2 + y^2 = R^2 兩側的弧長是
ds = √(1+y^2/x^2) dy
所以, 圓周長是
∫_[-R,R] 2√(1+y^2/x^2) dy
= ∫_[-R,R] 2R/|x| dy
= ∫_[-R,R] 2R/√(R^2-y^2) dy
= ∫_[-π/2,π/2] (2/cosθ) Rcosθ dθ
= 2πR
現在來看球面 x^2+y^2+z^2 = R^2 的表面積
問題. 從 z 到 z+dz, 球面接近一個兩底半徑分
別是 √(R^2-z^2) 與 √[R^2-(z+dz)^2] , 高 dz
的`圓錐台, 其斜高約 [R/√(R^2-z^2)] dz, 其側
表面積約 2π√(R^2-z^2) [R/√(R^2-z^2)] dz
故, 球表面積為
∫_[-R,R] 2π√(R^2-z^2) [R/√(R^2-z^2)] dz
= 2πR ∫_[-R,R] dz
= 4πR^2
A:
還是先用 圓 x^2 + y^2 = R^2 來說吧.
從 y 到 y+dy, 圓 x^2 + y^2 = R^2 是不是被切出
左右兩段弧:
╭ ╮
把上下底分別連上, 是不是近似一個等腰梯形?
如果 y 變成 z, 圓方程式改成 x^2 + z^2 = R^2
繞 z 軸轉半圈, 不就是球 x^2 + y^2 + z^2 = R^2
了嗎? 而上述 "梯形" 旋轉後不就是一個圓錐台?
=====================================
首先, ∫_[-R,R] 2πy dz 這式就有點問題.
先不談求面積, 看圓周長, 如果用
∫_[-R,R] 2 dy
能算出圓周長嗎? 不! 當 y 變為 y+dy 時,
圓 x^2 + y^2 = R^2 兩側的弧長是
ds = √(1+y^2/x^2) dy
所以, 圓周長是
∫_[-R,R] 2√(1+y^2/x^2) dy
= ∫_[-R,R] 2R/|x| dy
= ∫_[-R,R] 2R/√(R^2-y^2) dy
= ∫_[-π/2,π/2] (2/cosθ) Rcosθ dθ
= 2πR
現在來看球面 x^2+y^2+z^2 = R^2 的表面積
問題. 從 z 到 z+dz, 球面接近一個兩底半徑分
別是 √(R^2-z^2) 與 √[R^2-(z+dz)^2] , 高 dz
的`圓錐台, 其斜高約 [R/√(R^2-z^2)] dz, 其側
表面積約 2π√(R^2-z^2) [R/√(R^2-z^2)] dz
故, 球表面積為
∫_[-R,R] 2π√(R^2-z^2) [R/√(R^2-z^2)] dz
= 2πR ∫_[-R,R] dz
= 4πR^2
2020-12-07 10:12 am
我沒辦法理解你怎麼用圓錐切的
收錄日期: 2021-05-04 02:32:48
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20201206101040AAaZeyT

