如附圖
請問x與y是否有實數解?
如果有,那要如何解出?
這是我讀微波工程時突然想出的問題,所以我也不知道答案。
含虛數的方程式,請問是否有實數解?
2020-12-02 7:50 pm
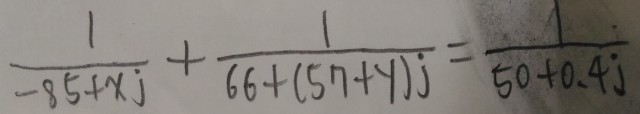
回答 (1)
2020-12-03 8:47 am
✔ 最佳答案
如果 j 是虛數單位 √(-1), 則...令 z = 57 + y. 假設 x, y, z 都是實數.
方程式可將分母實數化:
(-85-xj)/(7225+x^2) + (66-zj)/(4356+z^2) = (50-0.4j)/(2500.16)
所以, 依複數相等之定義:
-85/(7225+x^2) + 66/(4356+z^2) = 50/2500.16
-x/(7225+x^2) -z/(4356+z^2) = -0.4/2500.16
把它看成是 1/(7225+x^2) 和 1/(4356+z^2) 的線性方程, 解得
2500.16/(7225+x^2) = (26.4-50z)/(66x+85z)
2500.16/(4356+z^2) = (34+50x)/(66x+85z)
化為多項式方程:
2500.16(66x+85z) = (7225+x^2)(26.4-50z)
= (4356+z^2)(34+50x)
要解這最後的方程組, 用數值解吧.
(利用線上軟體繪圖, 得一解: x = -0.68, z = 0.528,
y = z - 57 = -56.472)

收錄日期: 2021-05-04 02:36:46
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20201202115011AAsUU3H

