1.已知平面上有A(0,0),B(-2,0),C(-2,4)三點,求線段BC的中垂線以及三角形ABC的外心
2.試求點A(3,6)對直線L:x+2y-5=0之投影點及對稱點
3.請問這題是對還錯?請說明原因
徵求數學高手~高一數學直線與圓問題(急)?
2020-11-25 5:02 pm
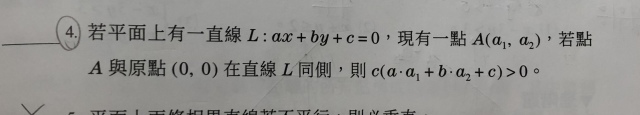
回答 (1)
2020-12-06 6:21 am
1.
AB 線: y = 0; AB 中點: (-1,0)
AC 線: y = -2x; AC 中點: (-1,2)
BC 線: x = -2; BC 中點: (-2,2)
中垂線就是過中點與該邊垂直的直線.
且兩線垂直, 若均有斜率, 則其斜率乘積為 -1.
故:
AB 邊之中垂線: x = -1;
AC 邊之中垂線: y = 2 + (x+1)/2;
BC 邊之中垂線: y = 2.
三角形 ABC 之外心即是三邊中垂線之交點,
即 (-1,2).
2.
A (3,6) 對 L: x + 2y - 5 = 0 之投影對稱點是 B,
則 L 是 AB線段之中垂線.
設 B 點座標 (a,b), 則
(b-6)/(a-3) = 2 (因 L 之斜率為 -1/2)
故
b = 6+2(a-3) = 2a
故 AB 線方程式為 y = 2x, 與 L 之交點為 C (1,2).
故
B = C + (C-A) = (1,2) + (1-3,2-6) = (-1,-2).
3.
點 (a_1,a_2) 與 (0,0) 在 L: ax+by+c = 0 同側,
即是:
a(a_1)+b(a_2)+c > 0 <==> a(0)+b(0)+c > 0,
a(a_1)+b(a_2)+c < 0 <==> a(0)+b(0)+c < 0
所以,
c ( a(a_1)+b(a_2)+c ) > 0.
AB 線: y = 0; AB 中點: (-1,0)
AC 線: y = -2x; AC 中點: (-1,2)
BC 線: x = -2; BC 中點: (-2,2)
中垂線就是過中點與該邊垂直的直線.
且兩線垂直, 若均有斜率, 則其斜率乘積為 -1.
故:
AB 邊之中垂線: x = -1;
AC 邊之中垂線: y = 2 + (x+1)/2;
BC 邊之中垂線: y = 2.
三角形 ABC 之外心即是三邊中垂線之交點,
即 (-1,2).
2.
A (3,6) 對 L: x + 2y - 5 = 0 之投影對稱點是 B,
則 L 是 AB線段之中垂線.
設 B 點座標 (a,b), 則
(b-6)/(a-3) = 2 (因 L 之斜率為 -1/2)
故
b = 6+2(a-3) = 2a
故 AB 線方程式為 y = 2x, 與 L 之交點為 C (1,2).
故
B = C + (C-A) = (1,2) + (1-3,2-6) = (-1,-2).
3.
點 (a_1,a_2) 與 (0,0) 在 L: ax+by+c = 0 同側,
即是:
a(a_1)+b(a_2)+c > 0 <==> a(0)+b(0)+c > 0,
a(a_1)+b(a_2)+c < 0 <==> a(0)+b(0)+c < 0
所以,
c ( a(a_1)+b(a_2)+c ) > 0.
收錄日期: 2021-05-04 02:33:29
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20201125090203AA3o4vI

