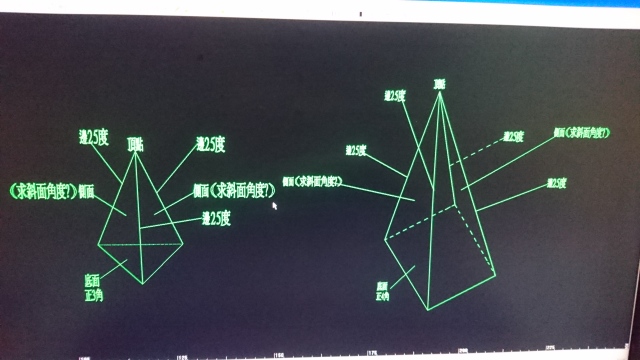
同理:正 3角椎 3個單邊各角為25度 ,求側面斜面角度算法。
已知邊夾角角度,求側面斜面角度。
謝謝
更新1:
求公式,謝謝
更新2:
請問33.4度是4角椎一面斜面的度數嗎? 我實物量起來怎麼好像是18度上下? 單邊稜線是25度(4角椎)
更新3:
4角椎18.25 3角椎13.12 怎麼來的...有算法嗎?抱歉,您寫的太過困難,看不懂,,,不好意思. 麻煩您了...
更新4:
有些複雜??,能否寫上數字算數....多少*多少,又,多少/多少?=18.25 謝謝,我學歷不高,不好意思
更新5:
雖然無法理解,但會用計算機按了,非常感謝