高二三角函數半角倍角問題?

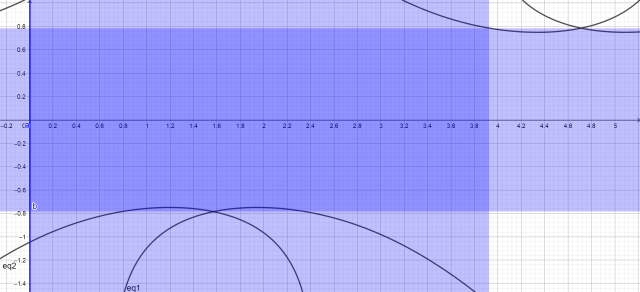
用軟體晝出兩方程式
    cos(x+y) = cos(x) + cos(y)
    cos(x-y)  = cos(x) - cos(y)
的圖形, 並限制
    0 ≦ x ≦ 1.25π, -0.25π ≦ y ≦ 0.25π
均可見兩方程式圖形都有部分在上列範圍.

cos(x+y) = cos(x) + cos(y)
<==> cos(x)cos(y) - sin(x)sin(y) = cos(x) + cos(y)
<==> (1-cos(x))cos(y) + sin(x)sin(y) = -cos(x)
令 z 使 
    sin(z) = (1-cos(x))/√[2(1-cos(x))]
    cos(z) = sin(x)/√[2(1-cos(x))]
則前列方程式在 cos(x) ≠ 1 條件下可改寫為
    sin(z+y) = -cos(x)/√[2(1-cos(x))]
例如, 取 x = 2π/3, 則 cos(x) = -1/2, sin(x) = √3/2,
    sin(z) = √3/2, cos(z) = 1/2
可令 z = π/6. 則得
    sin(y+π/6) = cos(π/3-y) = √3/6
因
    y = 0 時 sin(π/6) = cos(π/3) = 1/2 > √3/6
    y = -π/4 時
       sin(-π/4+π/6) = cos(π/3+π/4) < 0 < √3/6
故, 存在 y, -π/4 < y < 0 使
    sin(y+π/6) = cos(π/3-y) = √3/6
即 
    cos(2π/3 +y) = cos(2π/3) + cos(y)

或者, 更直接地, 我們在取 x = 2π/3 之下, 想知道
是否存在 y 在 [-π/4,π/4] 區間內, 使
    cos(x+y) = cos(x) + cos(y)
即 cos(2π/3+y) = cos(2π/3) + cos(y).
考慮 y = 0 時, 得
    cos(2π/3+0) < cos(2π/3) + cos(0)
而 y = -π/4 時,
    cos(2π/3 - π/4) = cos(5π/12) = sin(π/12)
        = √[(1-cos(π/6))/2] = √(1/2-√3/4) ≒ 0.2588
    cos(2π/3) + cos(-π/4) = -1/2 + √2/2 ≒ 0.2071
故 cos(2π/3 - π/4) > cos(2π/3) + cos(-π/4).
因此, 存在 y, -π/4 < y < 0, 使
    cos(x+y) = cos(x) + cos(y).


對於 cos(x-y) = cos(x) - cos(y), 取 x = π/3, 我們
想驗證存在 y 在 [-π/4,π/4] 之間, 使方程式成立.
同樣, 考慮 y = 0 和 y = -π/4 兩點.

當 y = 0 時
    cos(π/3 - 0) = cos(π/3) > cos(π/3) - cos(0).

當 y = -π/4 時,
    cos(π/3 +π/4) = cos(7π/12) = -sin(π/12)
       ≒ -0.2588
    cos(π/3) - cos(-π/4) = 1/2 - √2/2 ≒ -0.2071

故, 必存在 y, -π/4 < y < 0, 使
    cos(x-y) = cos(x) - cos(y).


註: 
以上在 x 給定下, 判斷存在 y 使方程式成立, 是應用
 "勘根定理":
設 F(y) 是 y 的連續函數.
若 F(y1) 與 F(y2) 一正一負, 則存在 y 介於 y1, y2
之間, 滿足 F(y) = 0.
因此,
設 f(y), g(y) 都是 y 的連續函數, 若在 y1, y2 兩點,
 f(y) 與 g(y) 兩函數值大小關係相反, 則必存在 y 介
於 y1, y2 之間, 使 f(y) = g(y).