Solving a limit without L'Hosptital's Rule?
2020-11-02 7:42 pm
I am not sure where I am even meant to start with this problem. I know with l'hosptital's rule this would result in 3/5, but how would I reach this answer without it? Any advice is appreciated! Thank you
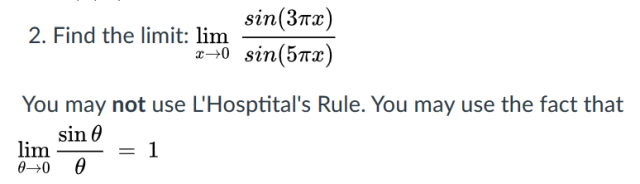
回答 (3)
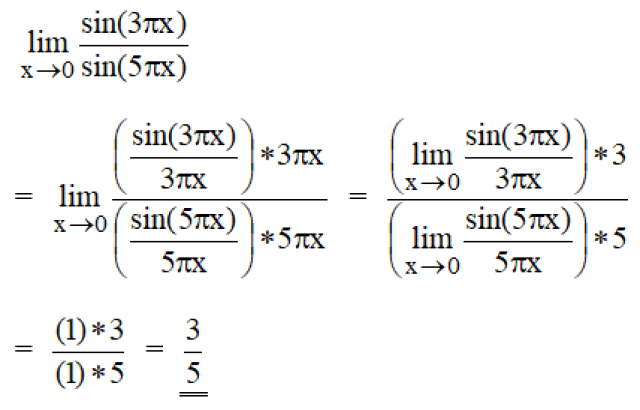
2020-11-02 8:43 pm
Answer: 3/5
lim x->0 sin(3πx)/sin(5πx) =
expand the fraction in following way
= lim x->0 (sin(3πx)/sin(5πx))*(3π/3π)*(5π/5π)*(x/x)
rearrange
= lim x->0 (3π*sin(3πx)/3πx)*((1/5π)*5πx/sin(5πx))
limit of product rule
= lim x->0 (3π*sin(3πx)/3πx) * lim x->0 ((1/5π)*5πx/sin(5πx))
factor out constants, 3π and 1/5π
= (3/5) * lim x->0 (sin(3πx)/3πx) * lim x->0 (5πx/sin(5πx))
now use the rule mentioned in the text to find
lim x->0 (sin(3πx)/3πx) = 1 and
lim x->0 (5πx/sin(5πx)) = 1
finally
lim x->0 sin(3πx)/sin(5πx) = (3/5)*1*1 = 3/5
lim x->0 sin(3πx)/sin(5πx) =
expand the fraction in following way
= lim x->0 (sin(3πx)/sin(5πx))*(3π/3π)*(5π/5π)*(x/x)
rearrange
= lim x->0 (3π*sin(3πx)/3πx)*((1/5π)*5πx/sin(5πx))
limit of product rule
= lim x->0 (3π*sin(3πx)/3πx) * lim x->0 ((1/5π)*5πx/sin(5πx))
factor out constants, 3π and 1/5π
= (3/5) * lim x->0 (sin(3πx)/3πx) * lim x->0 (5πx/sin(5πx))
now use the rule mentioned in the text to find
lim x->0 (sin(3πx)/3πx) = 1 and
lim x->0 (5πx/sin(5πx)) = 1
finally
lim x->0 sin(3πx)/sin(5πx) = (3/5)*1*1 = 3/5
2020-11-02 8:09 pm
lim sin(3πx)/sin(5π)
= lim sin(3πx)/(3πx) × (5πx)/sin(5πx) × (3πx)/(5πx)
= (1) × (1) × lim (3πx)/(5πx)
= 3/5
= lim sin(3πx)/(3πx) × (5πx)/sin(5πx) × (3πx)/(5πx)
= (1) × (1) × lim (3πx)/(5πx)
= 3/5
收錄日期: 2021-04-25 13:54:47
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20201102114211AAMPPjH