急！！！ 請問這題怎麼解?

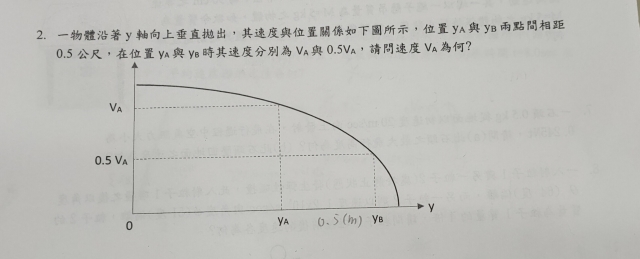
題目符號用得不好, "沿著 y 軸向上垂直拋出"?
附圖卻又把橫軸標示為 "y"?

其實應該說 "向上垂直拋出" 就好了!

所以, 時間 t 時的向上速度應是:
    v(t) = v_0 - gt
v_0 是上拋初速, 即 v(0); g 是重力加速度, 9.80665m/s^2.
假設初始位置 y(0) = 0, 則時間 t 時的位置是:
    y(t) = v_0 t - (g/2)t^2

故速度 v 對應時間
    t = (v_0 - v)/g
則位置與速度的關係是
    y = v_0(v_0-v)/g - (g/2)(v0-v)^2/g^2
      = (v_0^2 - v^2)/(2g)

故
    y_A = (v_0^2 - v_A^2)/(2g)
    y_B = (v_0^2 - 0.25 v_A^2)/(2g)
則
    0.5 = y_B - y_A
        = 0.75 v_A^2/(2g)
∴ v_A^2 = 2g(0.5/0.75) = 13.0755
   v_A = √13.0755 = 3.616 m/s
即: 每秒 3.616 公尺.