請各位幫幫我解題物理?

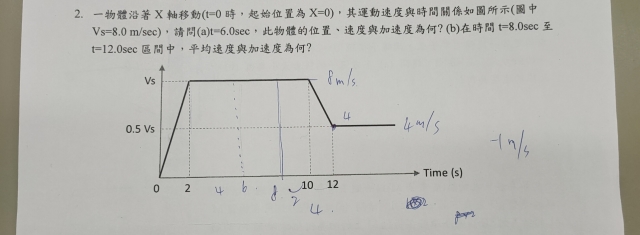
t = 0 至 t = 2, 速度(速率)從 0.0 m/sec 直線增
至 8.0 m/sec; 而後維持此速度至 t = 1o; 再然後
直線下降至 t = 12 的 4.0 m/sec; 最後維持等速
4.0 m/sec.

等加速度直線運動之位置公式:
s(t) = s(t0) + v(t0)(t-t0) + (a/2)(t^2-t0^2)
式中 s(t) 代表時間 t 時的位置, 0 是開始作等加
速度運動時間, v(t0) 是起始(時間t0時)速度, a
是加速度.

從 t = 0 時 v(0) = 0 至 t = 2 時 v(2) = 8.0,
是等加速度直線運動, 因此加速度是
    a = (8.0 - 0)/2 = 4.0 (m/sec^2)
又 s(0) = 0, 所以
    s(2) = (4.0/2)2^2 = 8 (m)

等速度運動位置公式則是
    s(t) = s(t0) + v(t-t0)
取 t0 = 2, t = 6, v = 8.0, 則
    s(6) = s(2) + 8.0(6-2)
         = 8 + 8.0(4)
         = 40 (m)

(a) t = 6(sec) 時位置離起點 40m,
    此時速度 8.0 m/sec,
    加速度 0.


t = 8 至 t = 10 速度是 8.0 m/sec, 等速;
t = 10 至 t = 12 速度從 8.0 直線降至 4.0,
平均速度 (8.0 + 4.0)/2 = 6.0 (m/sec).
所以, 從 t = 8 至 t = 12 的總平均速度是
    (8.0×2 + 6.0×2)/(2+2) = 7.0 (m/sec)

t = 8 至 t = 10 是等速運動, 加速度是 0.
t = 10 至 t = 12 的加速度是常數, 等於
    (4.0 - 8.0)/2 = -2.0 (m/sec^2)
t = 8 至 t = 12 整體來看非等速也非等加速度,
若論其平均加速度, 則是
    [0×2 + (-2.0)×2]/(2+2) = -1.0 (m/sec^2)