r+ln(0.05/r)=0.00485，r=?

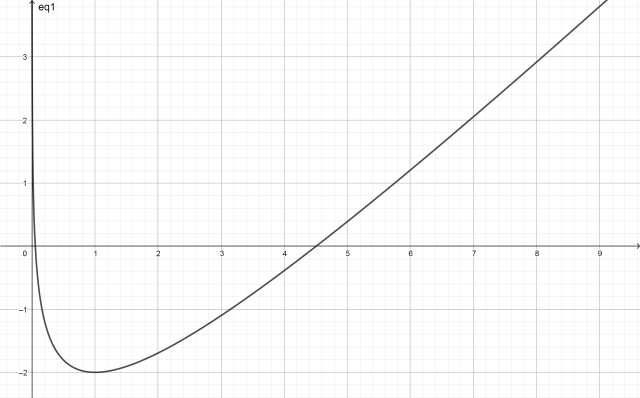
似乎只能數值解.
令 f(x) = x + ln(0.05/x) - 0.00485
則 f'(x) = 1 - 1/x
f(x) 定義於 x > 0, 有最小值
     f(1) = 0.99515+ln(0.05) ≒ -2 < 0
又:
    x → 0+, 則 f(x) → +∞
    x → +∞, 亦可得 f(x) → +∞
因此, f(x) = 0 有二根, 一根在 (0,1) 區間內,
另一根大於 1.

數值解法可考慮牛頓法:
    x1 = x0 - f(x0)/f'(x0)
式中 x0 是根之近似值, x1 是改進之近似值.

介於 0-1 之間的根需要較小的初值, 明碓地說, 選
正確根左邊或很靠近正確根才不致發散. 例如, 取 
x0 = 0.00001, 最後收斂至 0.052436865 .

大於 1 的根只要取大於1 的初值, 例如取 1.1, 2,
或 12345 都收斂到 4.505989867 .