How do I solve this derivative question?

Since g(x) = 2x + 1
f[g(x)] = f(2x + 1)
  
Then
h(x) = f(2x + 1)
  
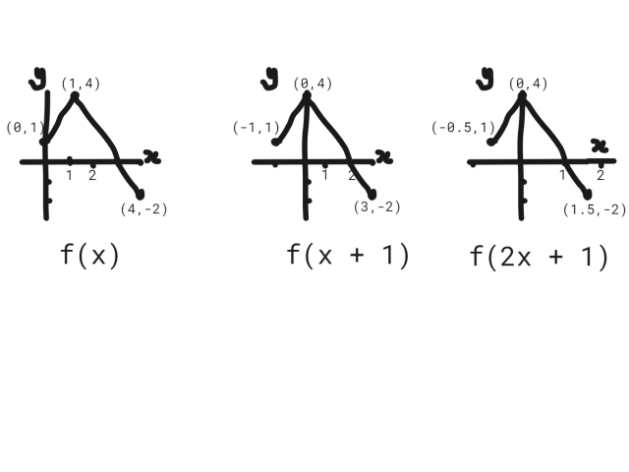
We are given f(x) on the graph, so we can transform it to f(2x + 1) as shown in the sketches below.
  
Then by inspection, at x = 1 the gradient is the slope of the downward line segment.
h'(1) = (y2 - y1)/(x2 - x1)
h'(1) = -6/1.5
h'(1) = -4 . . . . . . . . ANSWER


We can also reason that if h'(1) does map onto the downward line segment, then adding 1 has no effect on the slope, but multiplying by 2 will make the slope twice as steep. And the original slope is -6/3 = -2, so that is OK.

[Added: Some answers say there isn't a single value for the slope at x = 1 but the graph in the question is for f(x) not h(x) ]

1.
Refer to the graph of the function f.
The slopes of f(x) at x = 1 are different in the two line segments.
When 0 < x ≤ 1: f(x) = m₁x + a
When 1 ≤ x ≤ 4: f(x) = m₂x + b, where m₁ ≠ m₂

When 0 < x ≤ 1:
h(x) = f[g(x)]
h(x) = f(2x + 1)
h(x) = m₁(2x + 1) + a
h(x) = 2m₁x + (m₁ + a)
h'(x) = 2m₁
h'(1) = 2m₁

When 1 ≤ x ≤ 4:
Similarly, h'(1) = 2m₂

As the values of h'(1) are different (2m₁ ≠ 2m₂) in the two line segments, h'(1) is nonexistent.

The answer: e. nonexistent.

The rise slope and fall slope are different.
E non existent.

Nonexistent .............ANS (Option E)

h(1) = f[g(1)] = f(2×1 + 1) = f(3) = 0
h(1 + k) = f[g(1 + k)] = f(2×(1+k) + 1) = f(3 + 2k) = -4k
h(1 + k) - h(1) = -4k
[h(1 + k) - h(1)]/k = -4
As k goes to zero, h'(1) goes to -4.
Answer is a.
This is true because IN THE NEIGHBORHOOD OF x=3, f ' (x) IS CONTINUOUS.

f(x) = (3x+1) if x</= 1 or (-2x+6) if x >/= 1
h(x) = f(g(x) 
h(x) = (3(2x+1) + 1 if (2x+1)</= 1
==> h(x) = 6x + 4 if 2x </= 0
or h(x) = (-2(2x+1) +6) if (2x+1)>/= 1
==> h(x) = (-4x +4) if 2x >/= 0
if x = 1 then 2x> 0
==> h(x) = -4x +4
==> h'(x) = - 4
==> h'(-1) = -4

h'(1)  is nonexistent