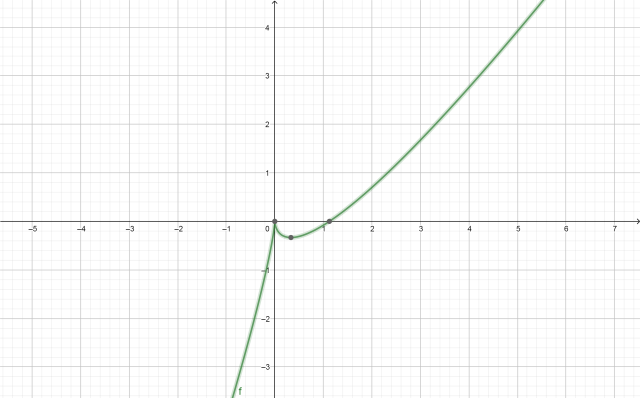
畫這個函數圖形判斷步驟可以詳細解釋嗎？f(x)=2x-(3x)^2/3,怎麼彎的可都說明嗎？

f(x) = 2x - (3x)^(2/3)

(1) 定義域
未明確指定的話, 就是自然定義域: 定義式可定義
的地方. 本例是整個數線 R.

(2) 截距
f(0) = 2(0) -0^(2/3) = 0
故其圖形通過原點.

f(x) = 2x^(2/3)x^(1/3) - 3^(2/3)x^(2/3)
      = x^(2/3)(2x^(1/3)-3^(2/3))
故 f(x) = 0 除 x = 0 一根外, 還有可能
    2x^(1/3) = 3^(2/3)
即: x = 3^2/2^3 = 9/8.

(3) 極限:
f(x) = x(2-3^(2/3)/x^(1/3))
當 x → ±∞ 時, 則 2-3^(2/3)/x^(1/3) → 2.
故整個 f(x) 隨 x 趨於 ±∞.

(註: 此處 f(x) 圖形並無漸近線. 雖然
       x → ±∞ 時 f(x)/(2x) → 1, 但
                         f(x) - 2x 並不趨近某常數.)

(4) 增減(升降)、極值
f'(x) = 2 - (2/3)(3x)^(-1/3)(3) = 2 - 2(3x)^(-1/3),
                                                                  x ≠ 0
故 
f'(x) = 0  <==>  2 = 2(3x)^(-1/3)  <==> x = 1/3.
且: 
0< x < 1/3 則 (3x)^(-1/3) > 1, 故 f'(x) < 0;
x > 1/3 則 (3x)^(-1/3) < 0, 故 f'(x) > 0
所以 f(1/3) = 2(1/3)-(3．1/3)^(2/3) = -1/3 是 
f(x) 的一個相對極小.

f(x) 還有一個臨界點 x = 0, 因 f(x) 在此點不可微.
而 x < 0 則 f'(x) > 0; 0 < x < 1/3 時 f'(x) < 0. 故
f(0) = 0 是 f(x) 的一個相對極大.

因 f(x) 上、下方皆無界, 所以並不存在絕對極值.

(5) 凹向 (彎曲方向):
當 x ≠ 0 時,
    f"(x) = 0 - 2(-1/3)(3x)^(-4/3)(3) 
           = 2(3x)^(-4/3)  > 0
故曲線在 x < 0 及 x > 0 兩部分都是凹面向上的.
(注意我們不能說曲線在整個 R 是凹面向上的.)