abs max and min?

f'(x)
= [(x² - x + 1) x' - x (x² - x + 1)'] / (x² - x + 1)²
= [(x² - x + 1) - x (2x - 1)] / (x² - x + 1)²
= [x² - x + 1 - 2x² + x] / (x² - x + 1)²
= (1 - x²) / (x² - x + 1)²
= (1 + x)(1 - x) / (x² - x + 1)²

When f'(x) = 0:  x = -1 or x = 1
Hence, relative maximum/minimum at x = -1 and x = 1

f(-1) = (-1) / [(-1)² - (-1) + 1] = -1/3 (= -7/21)
f(1) = 1/(1² - 1 + 1) = 1
f(-2) = (-2) / [(-2)² - (-2) + 1] = -2/7 (= -6/21)
f(3) = 3/(3² - 3 + 1) = 3/7

-1/3 < -2/7 < 3/7 < 1.  Hence,
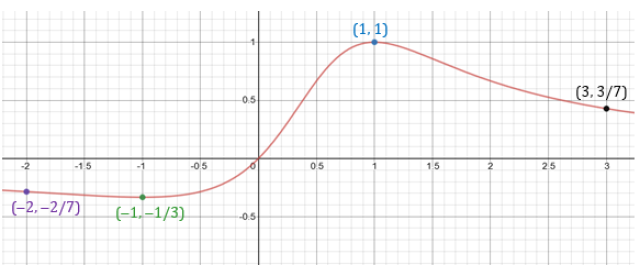
Absolute maximum value of f(x) = 1 when x = 1
Absolute minimum value of f(x) = -1/3 when x = -1

abs min at (-1, -1/3) and abs max at (1, 1)
Used my Ti-84 graphing