f（x）=2x/√x^2+1,畫出函數圖形，再沿圖形向右邊及左邊定出各一條水平漸進線，答案y=正負2,可以說明一下嗎？

f(x) = 2x/√(x^2+1)

首先, 這函數在所有實數點都可定義, 所以它的 "自然定義域"
是整個數線 R.

其次, 我想你要做的不是單純描點作圖, 而是應用微積分的方
法, 了解曲線特性, 而後利用這些特性把曲線描繪出來.

首先考慮截距:
x-截距: y = f(x) = 0 <==> x = 0, 所以此曲線通過原點, 同時
也說明了其 y-截距是 0.

對稱性:
對任意 x, f(-x) = - f(x).
所以這是一個 "奇函數", 也就是說它的圖形對稱於原點.

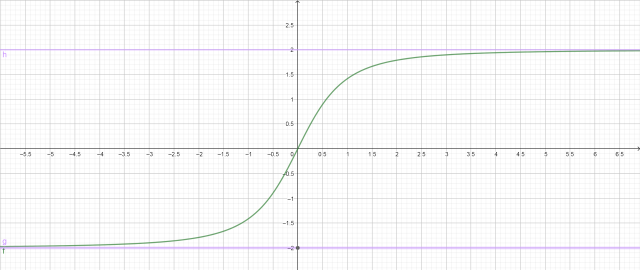
漸近線:
x → -∞ 則  f(x) = -2/√(1+1/x^2) → -2;
x → +∞ 則 f(x) = 2/√(1+1/x^2) → 2.
所以有兩條水平漸近線:
    y = -2  及  y = 2


增減、極值, 及凹向:

f'(x) = 2/√(x^2+1) + 2x(-1/2)(x^2+1)^(-3/2)(2x)
       = [2(x^2+1)-2x^2](x^2+1)^(-3/2)
       = 2(x^2+1)^(-3/2) ＞ 0 for all x.
所以 f(x) 是恆上升的, 沒有相對或絕對極值.

f"(x) = 2(-3/2)(x^2+1)^(-5/2)(2x)
       = -6x(x^2+1)^(-5/2)
f"(x) > 0 if x < 0;    f"(x) < 0 if x > 0.
所以: x < 0 時曲線是凹面向上的; x > 0 時則是凹面向下.
(0,0) 是曲線的反曲點.