f（x）=1+√x^2-4x+3圖形怎麼畫？因為我做題目有選項limx從左側趨近3,但答案是不存在，從右側趨近是1，表示圖形有畫空心的部分但不知道畫出來怎麼樣，幫忙一下感謝?

假設題目是:
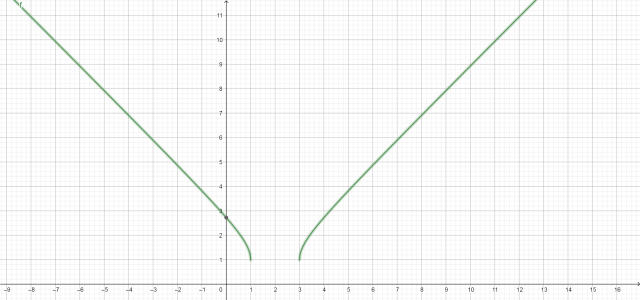
f(x) = 1 + √(x^2-4x+3)

函數曲線畫圖首先要考慮的是它的定義域.

在實數系, 根號裡不能是負數. 所以 f(x) 的定義域是:
D = { x : x^2-4x+3 ≧ 0 }.

因為  x^2-4x+3 = (x-1)(x-3), 
x^2-4x+3 ≧ 0 <==> x ≦ 1 或 x ≧ 3.

所以 f(x) 的定義域是兩個區間的聯集:
D = (-∞, 1] ∪ [3, ∞)

由於在 1 的右邊, 3 的左邊, 也就是在 (1, 3) 函數無
定義, 因此左段曲線畫至 x = 1 的位置, 終點 (1,1) 在
曲線上, 也就是說這一點是實心的. 同樣, (3,1) 也在
曲線上, 是右段的起點, 所以也是實心的.

因為在 1 的右邊鄰近, 及 3 的左邊鄰近, 函數並無定
義, 所以 "x 從右邊逼近 1" 或 "x 從左邊逼近 3" 時 f(x)
的單邊極限都無法定義, 當然是 "不存在".