等比數列問題,請各位數學大大解答!!!?
2020-10-09 11:21 pm
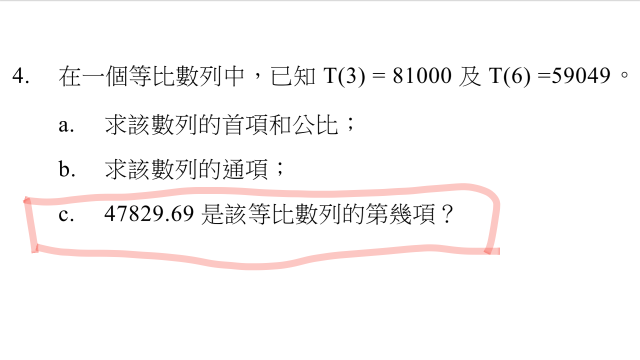
請各位數學大大解答(c)項,謝謝!!
回答 (2)
2020-10-10 8:01 am
設首項為 a, 公比為 r, 則此數列為
a, ar, ar^2, ...
第 n 項, 也就是一般項是 ar^(n-1)
所以:
T(6)/T(3) = r^3 = 0.729,
∴ r = 0.9
a = T(3)/0.9^2 = 1ooooo
∴ 第 n 項是
T(n) = 1ooooo (0.9)^(n-1), n = 1, 2, ...
478...9 = 1ooooo (0.9)^(n-1)
∴ (0.9)^(n-1) = 0.478...9
∴ n - 1 = log(0.478...9)/log(0.9)
log(0.4) = -1 + 2log(2) = -0.39794
log(0.5) = -log(2) = -0.3o1o3
∴ log(0.478...9) ≒ -0.322
log(0.9) = -1+2log(3) = -0.045758
∴ n - 1 = 7
∴ n = 8
驗證:
第8項是
T(8) = T(6)×r^2 = 59049×0.81 = 478...9
無誤.
說明: 由於 yahoo 的 "文字獄", 花了很多時間才修改成
可被看到的形式, 所以最後一題也無法寫出完整數字,
只能用刪節號處理. 最先回答的回答者用加減數字的
表現法, 昨日的回答者用概數法, 都是 yahoo 文字獄所
致. 大陸那邊一大堆被屏蔽字詞也就算了, 誰叫人家是
極權專制政體; 號稱自由民主的台灣, 也搞文字獄, 令
人愈來愈火大.
a, ar, ar^2, ...
第 n 項, 也就是一般項是 ar^(n-1)
所以:
T(6)/T(3) = r^3 = 0.729,
∴ r = 0.9
a = T(3)/0.9^2 = 1ooooo
∴ 第 n 項是
T(n) = 1ooooo (0.9)^(n-1), n = 1, 2, ...
478...9 = 1ooooo (0.9)^(n-1)
∴ (0.9)^(n-1) = 0.478...9
∴ n - 1 = log(0.478...9)/log(0.9)
log(0.4) = -1 + 2log(2) = -0.39794
log(0.5) = -log(2) = -0.3o1o3
∴ log(0.478...9) ≒ -0.322
log(0.9) = -1+2log(3) = -0.045758
∴ n - 1 = 7
∴ n = 8
驗證:
第8項是
T(8) = T(6)×r^2 = 59049×0.81 = 478...9
無誤.
說明: 由於 yahoo 的 "文字獄", 花了很多時間才修改成
可被看到的形式, 所以最後一題也無法寫出完整數字,
只能用刪節號處理. 最先回答的回答者用加減數字的
表現法, 昨日的回答者用概數法, 都是 yahoo 文字獄所
致. 大陸那邊一大堆被屏蔽字詞也就算了, 誰叫人家是
極權專制政體; 號稱自由民主的台灣, 也搞文字獄, 令
人愈來愈火大.
2020-10-11 8:45 am
r=0.9, 第6項59..., 第7項大約53...., 第8項就大約47到48,而且 0.9x0.9=0.81, T(6)尾數是9,乘以0.81尾數也是9,所以必定是第8項(此法用於選擇題)
收錄日期: 2021-05-03 20:38:01
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20201009152139AAACk6V


