已知x為有理數 x^2-5,x^2,x^2+5皆為有理數的平方 求x為多少?
2020-10-09 10:42 am
回答 (1)
2020-10-10 10:43 am
在 x > 0 條件下, 我只找到一個解: x = 41/12.
顯然: 若 x 是一解, 則 -x 亦是一解.
想不出簡單解法, 也未能真正證明 x > 0 的解唯一. 但幾乎
可確定上述解是唯二的. 以下若不嫌囉嗦, 可參考一下.
設 x^2-5 = (x-r)^2, x^2+5 = (x+s)^2, r, s 皆為有理數
因 x^2 - 5 是平方數, 所以 x^2 > 5.
若一有理數 x 滿足條件, 則 -x 亦滿足. 所以, 暫時限定討
論 x > 0 的情形.
設 x = n/m, r = q/p, s = v/u.
則得
5 = x^2-(x-r)^2 = (2x-r)r = (2n/m-q/p)(q/p)
= (x+s)^2-x^2 = (2x+s)s = (2n/m+v/u)(v/u)
故
5mp^2 = (2np-mq)q
5mu^2 = (2nu+mv)v
由前者, 因 m 與 n, p 與 q 分別互質, 故
q 整除 5m, m 整除 2p.
由後者,
v 整除 5m, m 整除 2u.
設 p = am/2 = abq/1o
∴ r = q/p = 1o/(ab), a, b 為正整數.
x^2 - 5 = (x-r)^2 = x^2 - 2rx + r^2
∴ x = (r^2+5)/(2r) = (1/2)r + (5/2)(1/r)
= 5/(ab) + ab/4
若 a, b 無限制, 實際上 ab 遍歷所有正整數.
∴ x = 5/N + N/4, N 正整數
可驗證上列 x 確實滿足 x^2 - 5 是有理數平方的要求.
又, x = (5-s^2)/(2s) = (5/2)(1/s)-(1/2)s,
其中 s = 1o/(cd), c, d 為正整數.
∴ x = cd/4 - 5/(cd) = M/4 - 5/M, M 正整數
可驗證上列 x 也滿足 x^2 + 5 是有理數平方的要求.
又: x > 0 可導出 M≧5; 要 x > √5, 則 M≧11.
所以: 存在正整數 M, N 使
x = M/4 - 5/M = N/4 + 5/N > 0
所以, M, N 必須滿足
(M-N)/4 = 5/M+5/N
或即 MN = 20(M+N)/(M-N).
給定 N, 則
M = 2x+√(4x^2+20) = 2x+2√(x^2+5)
= 2(N/4+5/N)+2√[(N/4+5/N)^2+5]
此式結果必須是正整數, 所以 N 並非任意. 實際計算,
在 N ≦ 3000 只找到 N = 12, M = 15, x = 41/12.
又, 當 N 大時,
M = N + 20/N + 2{√[(N/4+5/N)^2+5] - (N/4+5/N)}
= N + 20/N + 2.5/{√[(N/4+5/N)^2+5] + (N/4+5/N)}
= N + 40/N + O(1/N^3)
因此, 太大的 N 應找不到配對的整數 M.
由 MN = 20(M+N)/(M-N),
若 M - N = 1, 則 M ≒ 40,
若 M - N = 2, 則 M ≒ 21.
一般 M-N = h 則
M ≦ 40/h + h
因 N 永遠小於 M, 可知 M, N 是有限的.
設 M ≒ N, 則
M^2 ≒ MN = (M+N).20/(M-N) ≒ M.40/(M-N)
∴ M ≒ 40/(M-N) ≦ 40
以上更闡明了 M, N 不可能太大.
下面附方程式 MN = 20(M+N)/(M-N) 的圖.
橫軸為 M. 縱軸為 N. 只考慮 M > N, 且 M, N > 0 即可.
要的是 (M,N) 為正整數對, 因此 M≧N+1≧2. 此處未能
展現, 但在放大圖形中可看到 M > 40 時, M < N+1.
顯然: 若 x 是一解, 則 -x 亦是一解.
想不出簡單解法, 也未能真正證明 x > 0 的解唯一. 但幾乎
可確定上述解是唯二的. 以下若不嫌囉嗦, 可參考一下.
設 x^2-5 = (x-r)^2, x^2+5 = (x+s)^2, r, s 皆為有理數
因 x^2 - 5 是平方數, 所以 x^2 > 5.
若一有理數 x 滿足條件, 則 -x 亦滿足. 所以, 暫時限定討
論 x > 0 的情形.
設 x = n/m, r = q/p, s = v/u.
則得
5 = x^2-(x-r)^2 = (2x-r)r = (2n/m-q/p)(q/p)
= (x+s)^2-x^2 = (2x+s)s = (2n/m+v/u)(v/u)
故
5mp^2 = (2np-mq)q
5mu^2 = (2nu+mv)v
由前者, 因 m 與 n, p 與 q 分別互質, 故
q 整除 5m, m 整除 2p.
由後者,
v 整除 5m, m 整除 2u.
設 p = am/2 = abq/1o
∴ r = q/p = 1o/(ab), a, b 為正整數.
x^2 - 5 = (x-r)^2 = x^2 - 2rx + r^2
∴ x = (r^2+5)/(2r) = (1/2)r + (5/2)(1/r)
= 5/(ab) + ab/4
若 a, b 無限制, 實際上 ab 遍歷所有正整數.
∴ x = 5/N + N/4, N 正整數
可驗證上列 x 確實滿足 x^2 - 5 是有理數平方的要求.
又, x = (5-s^2)/(2s) = (5/2)(1/s)-(1/2)s,
其中 s = 1o/(cd), c, d 為正整數.
∴ x = cd/4 - 5/(cd) = M/4 - 5/M, M 正整數
可驗證上列 x 也滿足 x^2 + 5 是有理數平方的要求.
又: x > 0 可導出 M≧5; 要 x > √5, 則 M≧11.
所以: 存在正整數 M, N 使
x = M/4 - 5/M = N/4 + 5/N > 0
所以, M, N 必須滿足
(M-N)/4 = 5/M+5/N
或即 MN = 20(M+N)/(M-N).
給定 N, 則
M = 2x+√(4x^2+20) = 2x+2√(x^2+5)
= 2(N/4+5/N)+2√[(N/4+5/N)^2+5]
此式結果必須是正整數, 所以 N 並非任意. 實際計算,
在 N ≦ 3000 只找到 N = 12, M = 15, x = 41/12.
又, 當 N 大時,
M = N + 20/N + 2{√[(N/4+5/N)^2+5] - (N/4+5/N)}
= N + 20/N + 2.5/{√[(N/4+5/N)^2+5] + (N/4+5/N)}
= N + 40/N + O(1/N^3)
因此, 太大的 N 應找不到配對的整數 M.
由 MN = 20(M+N)/(M-N),
若 M - N = 1, 則 M ≒ 40,
若 M - N = 2, 則 M ≒ 21.
一般 M-N = h 則
M ≦ 40/h + h
因 N 永遠小於 M, 可知 M, N 是有限的.
設 M ≒ N, 則
M^2 ≒ MN = (M+N).20/(M-N) ≒ M.40/(M-N)
∴ M ≒ 40/(M-N) ≦ 40
以上更闡明了 M, N 不可能太大.
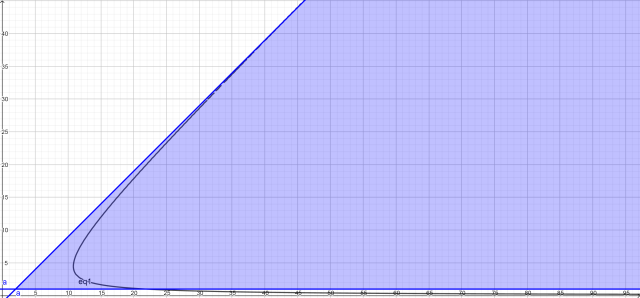
下面附方程式 MN = 20(M+N)/(M-N) 的圖.
橫軸為 M. 縱軸為 N. 只考慮 M > N, 且 M, N > 0 即可.
要的是 (M,N) 為正整數對, 因此 M≧N+1≧2. 此處未能
展現, 但在放大圖形中可看到 M > 40 時, M < N+1.
收錄日期: 2021-05-04 02:30:15
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20201009024237AAQFMVH

