Could someone prove the theory below? thx?
2020-09-25 10:53 pm
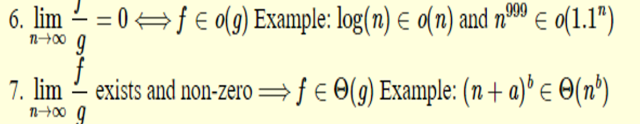
回答 (1)
2020-09-26 2:06 am
你的 o(g), Θ(g) 是怎樣定義的?
6. 可以說就是 o(g) 的定義了.
或許有的定義上形式上不是寫 lim f(n)/g(n) = 0,
例如寫:
For all c > 0, there exists N such that
if n ≧ N then |f(n)| < c |g(n)|
( 也就是 |f(n)/g(n)| < c )
但這不就是 lim f(n)/g(n) = 0 的定義嗎?
7. 與 Θ(g) 的定義也就不過差在 Θ(g) 的定義不要求
f(n)/g(n) 必須有極限, 只要求 "同等級變化" 罷了.
Def.: f(n) = Θ(g(n)) as n → ∞ if
f(n) = O(g(n) and g(n) = O(f(n)) as n → ∞.
Def.:
f(n) = O(g(n)) (或如你貼出的寫法: f(n) belong to g(n))
if there exist M > 0 such that |f(n)| ≦ M |g(n)| for all large n.
若 lim f(n)/g(n) = c 存在且不為 0, 則依極限之定義,
there exists N such that
|c|/2 < |f(n)/g(n)| < 3|c|/2 when n ≧ N
因此,
|f(n)| ≦ (3|c|/2) |g(n)|, ∴ f(n) = O(g(n));
|g(n)| ≦ (2/|c|) |f(n)|, ∴ g(n) = O(f(n)).
也就是說: f(n) = Θ(g(n)).
以上考慮一般函數. 所以用到絕對值. 如計算機演算法上
時間複雜度的函數都是 positive value, 則絕對值符號可
省掉, big-O 的定義中 "for large n" 也可改成 "for all n".
6. 可以說就是 o(g) 的定義了.
或許有的定義上形式上不是寫 lim f(n)/g(n) = 0,
例如寫:
For all c > 0, there exists N such that
if n ≧ N then |f(n)| < c |g(n)|
( 也就是 |f(n)/g(n)| < c )
但這不就是 lim f(n)/g(n) = 0 的定義嗎?
7. 與 Θ(g) 的定義也就不過差在 Θ(g) 的定義不要求
f(n)/g(n) 必須有極限, 只要求 "同等級變化" 罷了.
Def.: f(n) = Θ(g(n)) as n → ∞ if
f(n) = O(g(n) and g(n) = O(f(n)) as n → ∞.
Def.:
f(n) = O(g(n)) (或如你貼出的寫法: f(n) belong to g(n))
if there exist M > 0 such that |f(n)| ≦ M |g(n)| for all large n.
若 lim f(n)/g(n) = c 存在且不為 0, 則依極限之定義,
there exists N such that
|c|/2 < |f(n)/g(n)| < 3|c|/2 when n ≧ N
因此,
|f(n)| ≦ (3|c|/2) |g(n)|, ∴ f(n) = O(g(n));
|g(n)| ≦ (2/|c|) |f(n)|, ∴ g(n) = O(f(n)).
也就是說: f(n) = Θ(g(n)).
以上考慮一般函數. 所以用到絕對值. 如計算機演算法上
時間複雜度的函數都是 positive value, 則絕對值符號可
省掉, big-O 的定義中 "for large n" 也可改成 "for all n".
收錄日期: 2021-05-04 02:31:14
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20200925145359AA6yocf

