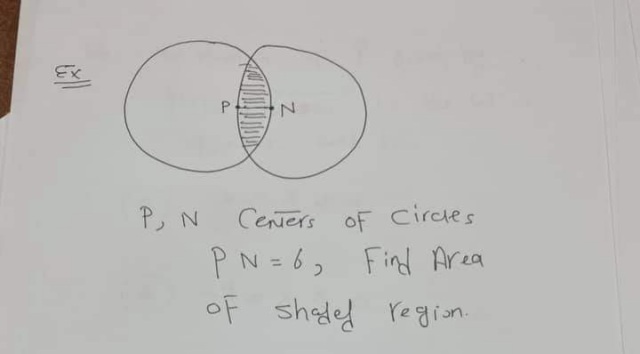
Can someone explain this question plz ?

Refer to the figure below.
The two circles meet at A and B. Join PA, PB, NA and NB.

PN is the common radius of the two circles.
Hence, radii PA = PB = PN = NA = NB = 6

ΔPAN and ΔPBN are equilateral triangles with each side = 6 and each angle = 60°

Area of ΔPAN
= Area of ΔPBN
= (1/2) × 6 × 6 × sin60°
= 18 × (√3/2)
= 9√3

Area of segment AP
= Area of segment BN
= Area of segment BP
= Area of segment AN
= (Area of sector PAN) - (Area of ΔPAN)
= 6π - 9√3

Area of the shaded region
= (Area of ΔPAN) × 2 + (Area of segment AP) × 4
= (9√3) × 2 + (6π - 9√3) × 4
= 18√3 + 24π - 36√3
= 24π - 18√3
≈ 44.3313

Bad calculator work 

Area =  24pi -18*sqrt(3)  (this is correct) 
but it does not equal  44.3313
It does equal this
Area =   44.22130915

So both answers which complete the problem 
using different methods 
really have the same solution if it weren't for a typo. or poor
calculator work  

One set of circle which meets this picture 

(x-6)^2 + (y-6)^2  = 36 
x^2  +  (y-6)^2  = 36   

center are  P  (0,6),   N  (6,6) 
Then, distance between center would be   
distance = sqrt ( 6^2 + 0^2 ) = sqrt(36) = 6 

Intersection   
x^2  + (y-6)^2  = (x-6)^2  + (y-6)^2 
x^2 =  x^2 -12x +36  
-12x + 36 = 0 
12x =36  
x = (36/12) = 3  

(3-6)^2 + (y-6)^2  = 36  
9 + (y-6)^2  =36 
(y-6)^2 =27
taking the square root of both sides
(y-6) =  +/- 3*sqrt(3)  
y-6 =  +/- 3*sqrt(3)   
y =   6 +/-  3*sqrt(3) 

The area of the shaded is 
the area of two chord topped 
circular segments.  
this is formula for the area of one of the segments 

 A=(R^2/2) ( theta - sin(theta) )  

R = 6 
R^2 = 36 
A (of one circular segment) = 18(theta-sin(theta) ) 

so (1/2)theta = arccos(  opp/hyp) = 
(1/2)theta   = arcos(3/ ( sqrt( ( (3-0)^2 + (6- (6 - 3*sqrt(3))^2) 
(1/2)theta = arcos(  3/   sqrt(  9  +  (3*sqrt(3)^2 ) 
(1/2)theta  = arcos(3/ sqrt(  9 + 9*3 ) 
(1/2) theta = arcos( 3/sqrt(36)  = arcos(1/2)   =pi/3 + 2pi 
or  -pi/3 + 2pi   
but the (1/2)theta  is less than pi/2  
(1/2)theta = pi/3 
theta = 2pi/3    
A(one circular segment) =  18( 2pi/3 - sin(2pi/3)  ) 
A(one circular segment) = 18(2pi/3 - sqrt(3)/2 )  
so but we have two circular segments 

All Area  = 36(2pi/3  - sqrt(3)/2)  = 44.22130915 square units 

Article on determining the area of a circular segment 

https://en.wikipedia.org/wiki/Circular_segment#:~:text=In%20geometry%2C%20a%20circular%20segment,a%20secant%20or%20a%20chord.


 

 Circle P and Circle N intersect such that line PN = 6. 
 The area of the shaded region:

Set up a rectangular coordinates system through P as center, with the x-axis 
coincident with PN & the y-axis through P. The circle P has equation as
x^2+y^2=36
=>
the area of the shaded part
.......6..............6
A=2S(2y)dx=4Ssqr(36-x^2)dx
.......3..............3
Let x=6sinB, then dx=6cosBdB
=>
.........pi/2
A=144Scos^2(B)dB
.........pi/6
=>
........pi/2
A=72S[cos(2B)+1]dB
........pi/6
=>

A=72[pi/3-sqr(3)/4]=24pi-18sqr(3)~44.2213.

P is a point --- the center of the left circle. = = = you put the point too far to the right.  
N is a point  --- the center of the circle on the right ===  Again -- this point is too for to the left.

  line PN is 6 unit long  ==== it is more than yu have drawn it.

The shaded part has a point at the top and bottom.  To solve the problem you need to put those points on the drawing and label them something  ... Maybe the top point is  A and the bottom point is B.  Whatever you want.  This allows you to draw some extra lines .. PA, PB, NA, NB, and AB.  ===  This makes some triangles,  actually, the larger triangles are isosceles.  Now us what you know and -- do the problem.  Looks like a Geometry problem == HS geometry was more than 50 years ago... Good luck.