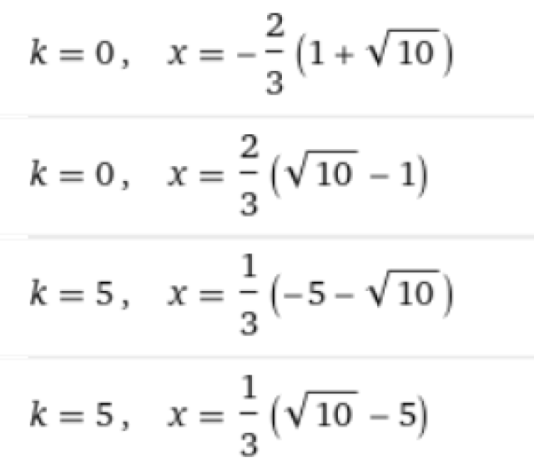Factor Theorem Algebra Questions?

1)
Let (m - n), m, (m + n) be the roots of the equation x³ + ax² + bx + c = 0

a = -[(m - n) + m + (m + n)]
a = -3m
Hence, m = -a/3

m is one of the roots of the equation x³ + ax² + bx + c = 0
Plug x = -a/3 into the equation x³ + ax² + bx + c = 0:
(-a/3)³ + a(-a/3)² + b(-a/3) + c = 0
(-a³/27) + (a³/9) - (ab/3) + c = 0
[(-a³/27) + (a³/9) - (ab/3) + c] * 27 = 0
-a³ + 3a³ - 9ab + 27c = 0
2a³ - 9ab + 27c = 0
Hence, 2a³ + 27c = 9ab

====
2.
This is a difficult question and cannot be solved by Factor Theorem.

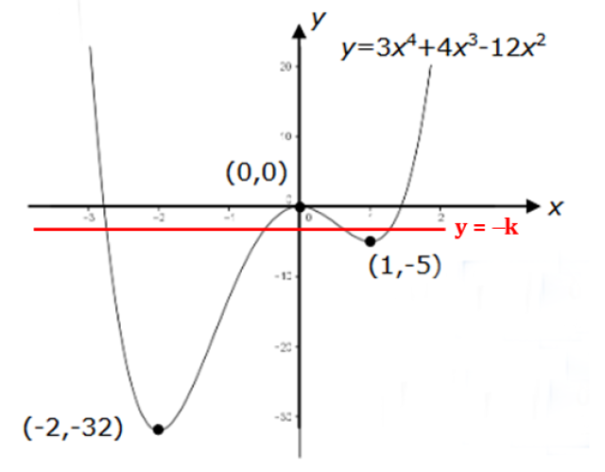
First of all, the stationary points of f(x) = 3x⁴ + 4x³ - 12x² are found by using differentiation.
f(x) = 3x⁴ + 4x³ - 12x²
f'(x) = 12x³ + 12x² - 24x = 12x(x + 2)(x - 1)
f"(x) = 36x² + 24x - 24

When x = 0:
f(0) = 3(0)⁴ + 4(0)³ - 12(0)² = 0
f'(0) = 0
f"(0) = 36(0)² + 24(0) - 24 = -24 < 0
Hence, maximum at (0, 0)

When x = -2:
f(-2) = 3(-2)⁴ + 4(-2)³ - 12(-2)² = -32
f'(-2) = 0
f"(-2) = 36(-2)² + 24(-2) - 24 = 72 > 0
Hence, minimum at (-2, -32)

f(1) = 3(1)⁴ + 4(1)³ - 12(1)² = -5
f'(1) = 0
f"(1) = 36(1)² + 24(1) - 24 = 36 > 0
Hence, minimum at (1, -5)

Sketch the graph y = 3x⁴ + 4x³ - 12x² as shown in the figure below.

Finally, solve the equation 3x⁴ + 4x³ - 12x² + k = 0
Then, 3x⁴ + 4x³ - 12x² = -k
The roots are the points of intersection of y = 3x⁴ + 4x³ - 12x² and y = -k
There are four points of intersection (i.e. four real roots) when -5 < -k < 0
Hence, 0 < k < 5  or  k ∊ (0, 5)

(When k = 0 or k = 5, there are only THREE points of intersection, i.e. THREE real roots.)

Here your answer:

1) 
The eqn x^3 + ax^2 + bx + c = 0 has 3 real roots 
and these roots are consecutive terms in an arithmetic progression. 
show that 2a^3 + 27c = 9ab.

2) Find the set of values of k for which the eqn 3x^4 + 4x^3 -12x^2 + k = 0 has four real roots.

( 1 )
x³ + ax² + bx + c = 0

let the roots be α, β and 𝛾 in that order

NOTE:
Remember the following;
➤ sum of roots, α + β + 𝛾
➤ sum of products of roots taken two at a time, αβ + β𝛾 + 𝛾α
➤ product of roots, αβ𝛾

α + β + 𝛾 = -a
αβ + β𝛾 + 𝛾α = b
αβ𝛾 = -c

Common Difference:
β - α = 𝛾 - β
∴2β = α + 𝛾
——————

Taking: α + β + 𝛾 = -a and replace α + 𝛾 with 2β
α + β + 𝛾 = -a
β + 2β = -a
∴β = -⅓a
——————

Taking: αβ𝛾 = -c, replace β with -⅓a
αβ𝛾 = -c
(-⅓a)α𝛾 = -c
∴α𝛾 = 3c/a
——————

Taking: αβ + β𝛾 + 𝛾α = b, and replace α + 𝛾 with 2β 
αβ + β𝛾 + 𝛾α = b
β( α + 𝛾 ) + 𝛾α = b
β( 2β ) + 𝛾α = b
2β² + 𝛾α = b
—————> let's replace 

2β² + 𝛾α = b
2( -⅓a )² + ( 3c/a ) = b
2a²/9 + 3c/a = b
2a² + 27c/a = 9b
2a³ + 27c = 9ab
━━━━━━━

The roots add up to –a, so they have the form a/3 – m, a/3, a/3 + m; this shows that if we shift the cubic a/3 to the left, i.e, if we apply the substitution x = u –a/3 to the cubic we shall get a cubic in u in which one of rhe roots is zero. Substituting:
0 = (u – a/3)³ + a(u – a/3)² + b(u – a/3) + c =
(1/27)(27u³ – 9a²u + 27bu + 2a³  + 27c +  – 9ab)
Since 0 is a root of this equation by construction,
we must have and 2a³  + 27c  – 9ab = 0 → 2a³  + 27c = 9ab.

your completely incorrect.

x^3+ax^2+bx+c certainly does NOT equal zero.

zero is a theroritical element that does not exist at all.

I suggest you go to your teacher and tell him/her to quit slacking and lying to you all about zero.

And tell them to learn to use math apportietey not just repiticiously by verbatim tell lies about zero to escape real work!

get hot now!