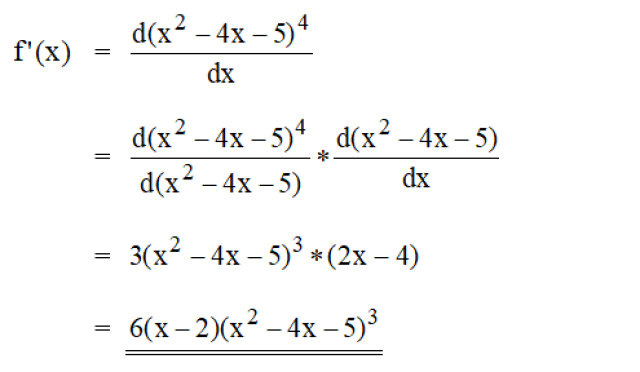f(x)=(x^2-4x-5)^4?
Derivatives
更新1:
Solve using chain rule
回答 (8)
Please read the following answer:
f(x) = (x^2 - 4x - 5)^4
d/dx((x^2 - 4 x - 5)^4) = 8 (x - 2) (x^2 - 4 x - 5)^3
Use the power rule and chain rule.
f(x) = (x^2 - 4x - 5)^4
f '(x) = 4(x^2 - 4x - 5)^3 * d/dx(x^2 - 4x - 5)
f '(x) = 4(x^2 - 4x - 5)^3 * (2x - 4)
f '(x) = (8x - 16)(x^2 - 4x - 5)^3
Yep, that's a chain rule problem alright. You have f(x) = u(v(x)) where u(x) = x^4 and v(x) = x^2 - 4x - 5. The chain rule says:
f'(x) = u'(v(x)) v'(x)
Since u'(x) = 4x^3 and v'(x) = 2x - 4, substituting gives you:
f'(x) = 4[v(x)]^3 * v'(x) = 4(x^2 - 4x - 5)^3 * (2x - 4)
= 8 (x - 2) (x^2 - 4x - 5)^3
It's a bit simpler to treat v as another dependent variable and just write out:
v = x^2 - 4x - 5
f(x) = v^4
df/dx = df/dv * dv/dx
= 4v^3 * (2x - 4) = 4(x^2 - 4x - 5)^3 * (2x - 4)
= 8(x - 2) (x^2 - 4x - 5)^3
f(x)=(x^2-4x-5)^4
=>
f '(x)=[4(x^2-4x-5)^3](2x-4)
=>
f '(x)=8(x-2)[(x-5)(x+1)]^3
Let u = ^2 - 4x - 5
Hence
du/dx = 2x - 4
Also
f(x) = y = u^4
dy/du = 4u^3
By the Chain Rule
dy/dx = dy/du x du/dx
dy/dx = 4u^3 X 2x - 4
Substitute
dy/dx = 4(x^2 - 4x - 5)^3 (2x - 4)
dy/dx = 4(2x - 4)(x^2 - 4x - 5)^3
dy/dx = (8x - 16)(x^2 - 4x - 5)^3
If you want to make the multiplication, then then second bracketed term has to be expanded by the Binomial Theorem.
f(x) = (x² - 4x - 5)⁴ → recall the derivative of u^(n) = n * u' * u^(n - 1)
f'(x) = 4 * (x² - 4x - 5)' * (x² - 4x - 5)³
f'(x) = 4 * (2x - 4) * (x² - 4x - 5)³
f'(x) = 8.(x - 2).(x² - 4x - 5)³
See this as derivative of outer expression*derivative of inner
f’(x) = (x^2 - 4x -5 )^3 *(2x – 4)
收錄日期: 2021-04-24 08:01:06
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20200903075652AAxC76J
檢視 Wayback Machine 備份