高職數學(三角函數)?
2020-09-02 1:52 am
有人可以告訴我這一題的算式嗎?
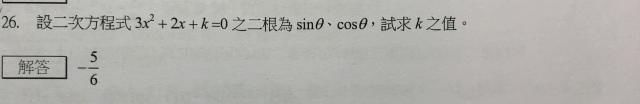
回答 (1)
2020-09-02 8:34 am
依根與係數的關係,
sinθ + cosθ = -2/3
sinθ × cosθ = k/3
故
2/3 = sinθ + cosθ
= √2(sinθ cos45° + cosθ sin45°)
= √2 sin(θ+45°)
所以
sin(θ+45°) = √2/3
θ + 45° = nπ + (-1)^n asin(√2/3), n 任意整數
(asin 是 反正弦函數)
∴ θ = nπ - 45° + (-1)^n asin(√2/3)
又,
k = 3 sin θ cosθ
= (3/2) sin(2θ)
= (3/2) sin(2[nπ - 45° + (-1)^n asin(√2/3)])
= (3/2) sin( 2(-1)^n asin(√2/3) - 90° ) (sin 週期 2π)
= -(3/2) cos( 2(-1)^n asin(√2/3) ) (sin(x-90°) = -cos(x))
= -(3/2) cos(2 asin(√2/3)) (cos(-x) = cos(x))
= -(3/2)(1-2sin^2(asin(√2/3)) (cos(2x) = 1-2sin^2(x))
= -(3/2)(1-4/9) (sin(asin(y)) = y)
= -(3/2)(5/9)
= -5/6
sinθ + cosθ = -2/3
sinθ × cosθ = k/3
故
2/3 = sinθ + cosθ
= √2(sinθ cos45° + cosθ sin45°)
= √2 sin(θ+45°)
所以
sin(θ+45°) = √2/3
θ + 45° = nπ + (-1)^n asin(√2/3), n 任意整數
(asin 是 反正弦函數)
∴ θ = nπ - 45° + (-1)^n asin(√2/3)
又,
k = 3 sin θ cosθ
= (3/2) sin(2θ)
= (3/2) sin(2[nπ - 45° + (-1)^n asin(√2/3)])
= (3/2) sin( 2(-1)^n asin(√2/3) - 90° ) (sin 週期 2π)
= -(3/2) cos( 2(-1)^n asin(√2/3) ) (sin(x-90°) = -cos(x))
= -(3/2) cos(2 asin(√2/3)) (cos(-x) = cos(x))
= -(3/2)(1-2sin^2(asin(√2/3)) (cos(2x) = 1-2sin^2(x))
= -(3/2)(1-4/9) (sin(asin(y)) = y)
= -(3/2)(5/9)
= -5/6
收錄日期: 2021-05-04 02:38:39
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20200901175222AAe6XRs

