（2547）8*（12）8請問八進制算法?

方法一:

2547₈ × 12₈
= (2×8³ + 5×8² + 4×8 + 7)₁₀ × (8 + 2)₁₀
= [(2×8³ + 5×8² + 4×8 + 7) × 8]₁₀ + [(2×8³ + 5×8² + 4×8 + 7) × 2]₁₀
= (2×8⁴ + 5×8³ + 4×8² + 7×8)₁₀ + [4×8³ + (8 + 2)×8² + 8×8 + (8 + 6)]₁₀
= (2×8⁴ + 5×8³ + 4×8² + 7×8)₁₀ + (4×8³ + 1×8³ + 2×8² + 1×8² + 1×8 + 6)₁₀
= (2×8⁴ + 5×8³ + 4×8² + 7×8)₁₀ + (5×8³ + 3×8² + 1×8 + 6)₁₀
= [2×8⁴ + (8 + 2)×8³ + 7×8² + 8×8 + 6]₁₀
= [(2×8⁴ + 1×8⁴) + 2×8³ + (7×8² + 1×8²) + 6]₁₀
= [3×8⁴ + (2×8³ + 1×8³) + 6]₁₀
= [3×8⁴ + 3×8³ + 0×8² + 0×8 + 6]₁₀
= 33006₈

====
方法二：

首先，將八進制數字轉換成十進
2547₈ = 2×8³ + 5×8² + 4×8 + 7 = 1383₁₀
12₈ = 1×8 + 2 = 10₁₀

然後，進行十進制乘法：
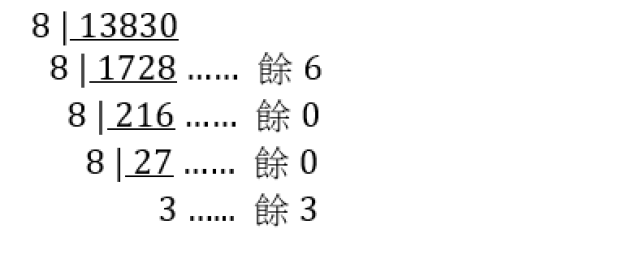
1383₁₀ × 10₁₀ = 13830₁₀

最後，用連續除法（如下圖）將答案轉換成八進制。
13830₁₀ = 33006₈
所以，2547₈ × 12₈ = 33006₈

(2547)8 × (12)8 兩 8進制數運算, 可如同十進制一般操作, 只是逢8進位.

    2 5 4 7
 ×       1 2
--------------
    5 3 1 6
 2 5 4 7
--------------
 3 3 0 0 6

所以, (2547)8 × (12)8 = (33006)8


細節:

(1)
(2547)8 × (2)8 部分:
    2 5 4 7
 ×          2
-------------
          1 6   =  (7)8 × (2)8 
        1 o     =  (4)8 × (2)8
     1 2        =  (5)8 × (2)8
     4
--------------
     5 3 1 6

(2)
       5 3 1 6
 + 2 5 4 7
-------------- --
                 6 
           1 o     =  (1)8 + (7)8 = (1o)8
           7        =  (3)8 + (4)8 = (7)8
     1 2           =  (5)8 + (5)8 = (12)8
     2
-----------------
     3 3 0 0 6      (注意 (1)8 + (7)8 = (1o)8 有進位)


總結: 同 n 進位制四則運算, 概如同十進制一般, 只是由加乘法的 
"逢十進位" 與減除法的 "(前一位)借 1 變(後一位值)十" 分別改成 
"逢 n 進位" 與 "借 1 值 n". 此處 n = 8, 乘法(內含)加法, 運算中就 
"逢8進位".