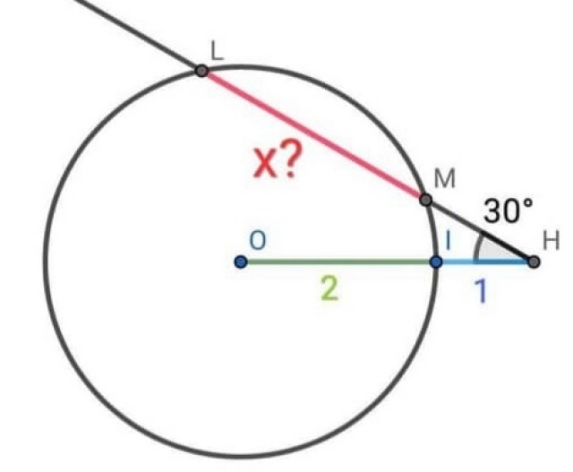
Geometry Problem?

Refer to the figure below.
Draw OP as shown which is the perpendicular bisector of LM.
Join OM. OM = 2 as OM is a radius of the circle.

In ΔHOP:
sin(30°) = OP/OH
OP = OH sin(30°)
OP = (1 + 2) × (1/20
OP = 3/2

In ΔOPM:
PM² + OP² = OM²  (Pythagorean theorem)
PM² + (3/2)² = 2²
PM² = 7/4
PM = (1/2)√7

x = 2 PM
x = 2 * (1/2)√7
x = √7
x ≈ 2.646

Drop perpendicular from O to meet LM at P. Note P bisects LM.

ΔOPH is a right-triangle: OP = (2+1)sin(30º) = 3/2

OM =2 (radius of circle) and PM=x/2, so in right-triangle ΔOMP:
PM² + OP² = OM²
(x/2)² + (3/2)² = 2²
which gives x = √7

In ∆OHL:

sin(θ)/3 = sin(30°)/2
sin(θ) = 3sin(30°)/2
sin(θ) = 3/4

cos²(θ) = 1 - (3/4)²
cos²(θ) = 7/16
cos(θ) = √(7)/4

sin(2θ)
= 2sin(θ)cos(θ)
= 2(3/4)√(7)/4
= 3√(7)/8

In ∆LOM:

LM/sin(∠OLM) = 2/sin(θ)
LM/sin(2θ) = 2/sin(θ)
LM = 2sin(2θ) / sin(θ)
LM = 2[3√(7)/8] / (3/4)
LM = √(7)