surd qns, hopefully can seek help help?
2020-08-21 10:16 pm
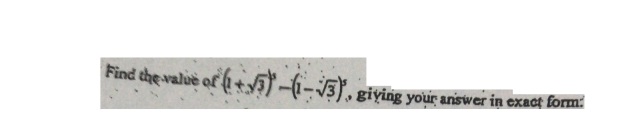
回答 (3)
2020-08-22 12:03 am
(a + b)⁵ = a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵ … [1]
(a - b)⁵ = a⁵ - 5a⁴b + 10a³b² - 10a²b³ + 5ab⁴ - b⁵ … [2]
[1] - [2]:
(a + b)⁵ - (a - b)⁵ = 10a⁴b + 20a²b³ + b⁵
Now, a = 1 and b = √3:
(1 + √3)⁵ - (1 - √3)⁵
= 10(1)⁴(√3) + 20(1)²(√3)³ + 2(√3)⁵
= 10√3 + 60√3 + 18√3
= 88√3
(a - b)⁵ = a⁵ - 5a⁴b + 10a³b² - 10a²b³ + 5ab⁴ - b⁵ … [2]
[1] - [2]:
(a + b)⁵ - (a - b)⁵ = 10a⁴b + 20a²b³ + b⁵
Now, a = 1 and b = √3:
(1 + √3)⁵ - (1 - √3)⁵
= 10(1)⁴(√3) + 20(1)²(√3)³ + 2(√3)⁵
= 10√3 + 60√3 + 18√3
= 88√3
2020-08-22 2:06 am
The expansions for (a+b)^5 and (a-b)^5 differ only in terms with an odd power of b. In subtracting these are doubled.
S = 10a^4 b + 20a^2 b^3 + 2b^5
a = 1, b = sqrt(3)
S = 10 sqrt(3) + 60 sqrt(3) + 18 sqrt(3)
S = 88 sqrt(3)
Before plugging in numbers, look for an algebraic simplification first.
S = 10a^4 b + 20a^2 b^3 + 2b^5
a = 1, b = sqrt(3)
S = 10 sqrt(3) + 60 sqrt(3) + 18 sqrt(3)
S = 88 sqrt(3)
Before plugging in numbers, look for an algebraic simplification first.
2020-08-21 10:44 pm
Is that:
(1 + √3)⁵ - (1 - √3)⁵
If so, then let's start with expanding them. Let's split them up into groups of squares:
(1 + √3)²(1 + √3)²(1 + √3) - (1 - √3)²(1 - √3)²(1 - √3)
Now simplify each squared term and simplify:
(1 + 2√3 + 3)(1 + 2√3 + 3)(1 + √3) - (1 - 2√3 + 3)(1 - 2√3 + 3)(1 - √3)
(4 + 2√3)(4 + 2√3)(1 + √3) - (4 - 2√3)(4 - 2√3)(1 - √3)
(4 + 2√3)²(1 + √3) - (4 - 2√3)²(1 - √3)
Do this again for the new squared factors, and simplify:
(16 + 16√3 + 4 * 3)(1 + √3) - (16 - 16√3 + 4 * 3)(1 - √3)
(16 + 16√3 + 12)(1 + √3) - (16 - 16√3 + 12)(1 - √3)
(28 + 16√3)(1 + √3) - (28 - 16√3)(1 - √3)
One more set of multiplications:
28 + 28√3 + 16√3 + 16 * 3 - (28 - 28√3 - 16√3 + 16 * 3)
28 + 44√3 + 48 - (28 - 44√3 + 48)
76 + 44√3 - (76 - 44√3)
Distribute the -1 and do the final simplification:
76 + 44√3 - 76 + 44√3
88√3
(1 + √3)⁵ - (1 - √3)⁵
If so, then let's start with expanding them. Let's split them up into groups of squares:
(1 + √3)²(1 + √3)²(1 + √3) - (1 - √3)²(1 - √3)²(1 - √3)
Now simplify each squared term and simplify:
(1 + 2√3 + 3)(1 + 2√3 + 3)(1 + √3) - (1 - 2√3 + 3)(1 - 2√3 + 3)(1 - √3)
(4 + 2√3)(4 + 2√3)(1 + √3) - (4 - 2√3)(4 - 2√3)(1 - √3)
(4 + 2√3)²(1 + √3) - (4 - 2√3)²(1 - √3)
Do this again for the new squared factors, and simplify:
(16 + 16√3 + 4 * 3)(1 + √3) - (16 - 16√3 + 4 * 3)(1 - √3)
(16 + 16√3 + 12)(1 + √3) - (16 - 16√3 + 12)(1 - √3)
(28 + 16√3)(1 + √3) - (28 - 16√3)(1 - √3)
One more set of multiplications:
28 + 28√3 + 16√3 + 16 * 3 - (28 - 28√3 - 16√3 + 16 * 3)
28 + 44√3 + 48 - (28 - 44√3 + 48)
76 + 44√3 - (76 - 44√3)
Distribute the -1 and do the final simplification:
76 + 44√3 - 76 + 44√3
88√3
收錄日期: 2021-04-24 07:56:57
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20200821141622AAMYtyL

