need help on part d and part e?

(d)
OB = OD = r = 4 cm

Arc BCD
= r × ∠BOD
= 4 × 1.7 cm
= 6.8 cm

Perimeter of the shaded region
= OB + OD + Arc BCD
= (4 + 4 + 6.8) cm
= 14.8 cm

====
(d)
Area of the shaded region
= Area of the sector OBCD
= r² × ∠BOD / 2
= 4² × 1.7 / 2 cm²
= 13.6 cm²

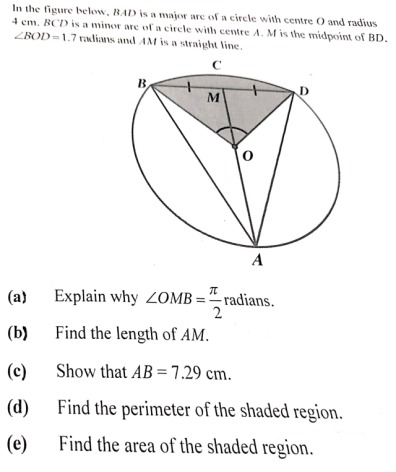
In the given figure, BAD is a major arc of a circle with center O and radius 4 cm. BCD is a minor arc of a circle with center A. M is the midpoint of BD. Angle BOD = 1.7 radians and AM is a straight line.
(a) Explain why angle OMB = pi/2 radians. 
(b) Find the length of AM.
(c) Show that AB= 7.29 cm.
(d) Find the perimeter of the shaded region. 
(e) Find the area of the shaded region.

So you know the length of OM, do you ?  Well, anyway, that will be 4 cos 0.85 = 2.64cm

And whilst we are with triangle OMB, BM = 4 sin 0.85 = 3.01 cm

So, in OMB, OM = 2.64 cm, BM = 3.01 cm and OB = 4 cm.

Now AM = AO + OM = 4 + 2.64 = 6.64 cm

and you presumably know that angle BAM = 0.85/2 = 0.425 rad.

Hence AB = AM/cos 0.425 = 7.288 cm

Since A is the centre of arc BCD, BA is the radius.
So length of arc BCD = 0.85 (7.288) = 6.195 cm.

And since OB and OD are both 4 cm, then perimeter of ABCD = 6.195 + 8 = 14.195 cm - answer (d).


Now, area of the SEGMENT BCD (make sure that you know exactly which bit I am talking about), with centre A = (sector ABCD) - (triangle ABD)

And the RADIUS of this sector = AB, which is 7.288 cm (see above) --- this is very important.

Sector area = 0.85/(2 pi) times (pi) AB^2
. . . . . . . . . . = (0.85/2) x 7.288^2 = 22.58 cm^2

Triangle area = BM x AM = 3.01 x 6.64 = 19.99cm^2

Hence area of segment BCD = 22.58 - 19.99 = 2.59

And area triangle BOD = BM x OM = 3.01 x 2.64 = 7.946

Therefore shaded area = 2.59 + 7.946 = 10.54 cm^2