Solution required?

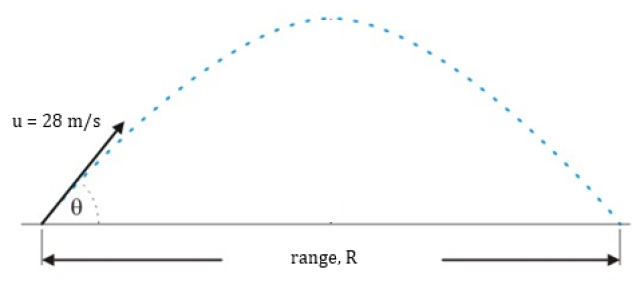
Refer to the figure below.
Take g = 9.8 m/s²

Consider the vertical motion when the ball hits the ground:
s(y) = u(y) t + (1/2) a(y) t²
0 = (28 sinθ) t + (1/2) (-9.8) t²
4.9t² = (28 sinθ)t
As t ≠ 0, thus 4.9t = 28 sinθ
Hence, t = (28/4.9) sinθ

Consider the horizontal motion when the ball hits the ground:
Range, R = (28 cosθ) t = (28 cosθ) (28/4.9 sinθ) = (28²/4.9) sinθ cosθ m

====
(a)
When θ = 30°:
Range, R = (28²/4.9) sin30° cos30° m = 69.3 m < 72 m
No, the ball will NOT cross the boundary.

====
(b)
When θ = 45°:
Range, R = (28²/4.9) sin45° cos45° m = 80 m > 72 m
Yes, the ball will cross the boundary.

====
(c)
When θ = 70°:
Range, R = (28²/4.9) sin70° cos70° m = 51.4 m < 72 m
No, the ball will NOT cross the boundary.

R1 = 28^2/g*sin (2*30°) = 0.866*28^2/9.807 = 69.2 m  ( NOOO !!)
R1 = 28^2/g*sin (2*45°) = 1*28^2/9.807 = 79.9 m ( YESSS !!)
R3 = 28^2/g*sin (2*70°) = 0.643*28^2/9.807 = 51.4 m ( NOOO !!)