Help, elevation question?

👨🏻‍🏫 學術台數學

[匿名]

2020-08-14 1:18 pm

A woman standing at point A looks up at the top of a building and finds the angle of elevation is 33∘. She walks 407 feet away from the building to point D and finds the angle of elevation to the top of the building is now 25∘.

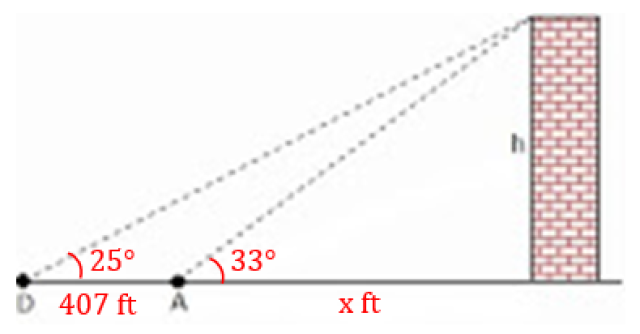
What is the height of the building h=___feet?

更新1:

https://lh3.googleusercontent.com/CRym0K9s2CeK9eNhVNxKIyw7nqjlmcdS2Iep1Ub91goa-74Z0QzWvm8QZ6NpsZRN91hD=s167

回答 (5)

micatkie

2020-08-14 3:28 pm

Refer to the figure below:

In the smaller right triangle:
tan33° = h/x
x = h/tan33° ...... [1]

In the larger right triangle:
tan25° = h/(x + 407)
x + 407 = h/tan25ᵖ
x = (h/tan25ᵖ) - 407 …… [2]

[1] = [2]:
h/tan33° = (h/tan25ᵖ) - 407
(h/tan25ᵖ) - (h/tan33°) = 407
h [(1/tan25ᵖ) - (1/tan33°)] = 407
h = 407 / [(1/tan25ᵖ) - (1/tan33°)] ft
h = 673 ft

The height of the building, h = 673 feet

👍 3 👎 0

ted s

2020-08-14 1:27 pm

you must be missing something as you state that at 407 from the building the angle is 25° ===> h = 407 tan 25°...want to update the query ?

👍 1 👎 2

Philip

2020-08-15 6:07 am

Put horizontal distance from base of building = d ft. & building height = h ft.;
h/d = tan33, ie., h = dtan33...(1).;
h/(d+407) = tan25, ie., h = (d+407)tan25...(2).;
By (1) & (2), dtan(33) = (d+407)tan25, ie., d(tan33-tan25) = 407tan25, ie, d =;
((407tan25)/(tan33-tan25)) ft = 1036.522579 ft and (1) now gives h = ;
1036.522579tan33 ft = 673.1256333 ft = 673 ft rounded off to nearest ft.

👍 0 👎 0

用戶69603

2020-08-14 9:54 pm

Draw a sketch of two interlinked right angle triangles and by using the 'sine rules' the height of the building works out as 673.1256332 feet or about 673 feet

👍 0 👎 0

Ian H

2020-08-14 3:49 pm

h/tan 25 = x + 407
h/tan 33 = x
h [1/tan 25 - 1/tan33)] = 407
h ~ 407/0.6046 ~ 673.1 feet

👍 0 👎 0

收錄日期: 2021-04-24 07:58:08
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20200814051830AAS1iWR

檢視 Wayback Machine 備份