Consider the triangle ABC with C=90∘. Compute the following trigonometric values when a=1 and b=5.
what does
sinA=
cosA=
sinB=
cosB=
need help asap?
2020-08-14 12:55 pm
回答 (6)
2020-08-14 3:41 pm
Refer to the figure below.
c² = a² + b² (Pythagorean theorem)
c = √(1² + 5²) = √26
sinA = a/c = 1/√26 = (√26)/26
cosA = b/c = 5/√26 = 5(√26)/26
sinB = b/c = 5/√26 = 5(√26)/26
cosB = a/c = 1/√26 = (√26)/26
c² = a² + b² (Pythagorean theorem)
c = √(1² + 5²) = √26
sinA = a/c = 1/√26 = (√26)/26
cosA = b/c = 5/√26 = 5(√26)/26
sinB = b/c = 5/√26 = 5(√26)/26
cosB = a/c = 1/√26 = (√26)/26
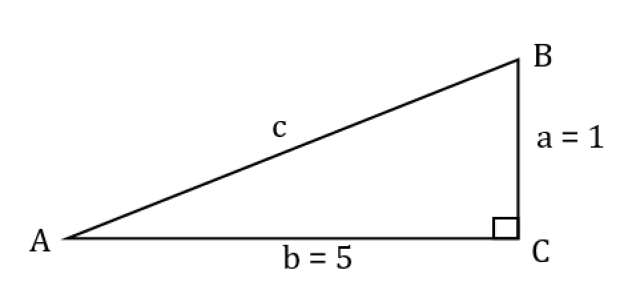
2020-08-14 1:12 pm
the reference triangle for angle A is { 5 , 1 , √26 } ...thus sin A = 1 / √26...you certainly can finish
2020-08-14 11:42 pm
Consider the triangle ABC with C = 90∘.
Compute the following trigonometric values when a = 1 and b = 5.
sin A =
cos A =
sin B =
cos B =
Compute the following trigonometric values when a = 1 and b = 5.
sin A =
cos A =
sin B =
cos B =
2020-08-14 6:31 pm
we 1st need to solve for the hypotenuse by using pythagorean theorem.
c = √(a^2 + b^2)
c = √(1^2 + 5^2)
c = √(26)
so
sin(A) = 1/√(26) or √(26)/26
cos(A) = 5/√(26) or 5√(26)/26
sin(B) = 5/√(26) or 5√(26)/26
cos(B) = 1/√(26) or √(26)/26
c = √(a^2 + b^2)
c = √(1^2 + 5^2)
c = √(26)
so
sin(A) = 1/√(26) or √(26)/26
cos(A) = 5/√(26) or 5√(26)/26
sin(B) = 5/√(26) or 5√(26)/26
cos(B) = 1/√(26) or √(26)/26
2020-08-14 5:01 pm
In triangle ABC, (A,B,C) is opposite (a,b,c) = (small arm,larger arm,hypotenuse)
Clearly, c^2 = a^2+b^2 = 1^2+5^2 = (rt26)^2, where rt = ''square root of''. Then
c = rt26.;
By law of sines, a/sinA = b/sinB = c/sinC;
c/sinC = rt26/sin90 = rt26/1 = rt26;
a/sinA = rt26, ie., sinA = a/rt26 = 1/rt26 = (1/26)rt26.;
b/sinB = rt26, ie., sinB = b/rt26 = 5/rt26 = (5/26)rt26.;
cos^2(A) = 1 - sin^2(A) = 1 - (1/26) = (25/26). Then cos(A) = (5/26)rt26.;
cos^2(B) = 1 - sin^2(B) = 1 - (25/26) = (1/26). Then cos(B) = (1/26)rt26.;
Clearly, c^2 = a^2+b^2 = 1^2+5^2 = (rt26)^2, where rt = ''square root of''. Then
c = rt26.;
By law of sines, a/sinA = b/sinB = c/sinC;
c/sinC = rt26/sin90 = rt26/1 = rt26;
a/sinA = rt26, ie., sinA = a/rt26 = 1/rt26 = (1/26)rt26.;
b/sinB = rt26, ie., sinB = b/rt26 = 5/rt26 = (5/26)rt26.;
cos^2(A) = 1 - sin^2(A) = 1 - (1/26) = (25/26). Then cos(A) = (5/26)rt26.;
cos^2(B) = 1 - sin^2(B) = 1 - (25/26) = (1/26). Then cos(B) = (1/26)rt26.;
2020-08-14 12:59 pm
Sohcahtoa
收錄日期: 2021-04-24 08:00:23
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20200814045525AA14fYe


